Introduction
This page, including the links on it give (hopefully) a complete enough description to make it simple (relatively) for anyone interested to make a complete PC receiver. The PC receiver described here is a two channel (stereo) system, and in combination with a cross yagi antenna it will automatically select optimum polarisation and filter tuning by a mouse click on the spectrum analyser graph presented on the computer screen.My interest is weak signal communication on 144MHz so my version is primarily for this purpose. The possible improvements on HF are much larger. Basically the PC receiver receives interference sources of all kinds in two channels at a large bandwidth and uses the information to cancel out the contribution from the different interference sources in the narrow passband in which the desired signal is present. In the process, each interference source is received with its own optimum phasing of the two channels to minimise noise.
For weak signal use on VHF the two channels are the two signals from a crossed yagi array, but on HF the two signals can be any two antennas that receive differently. Rather than adaptive polarisation the PC receiver would then use adaptive direction finding for signal and noise sources.
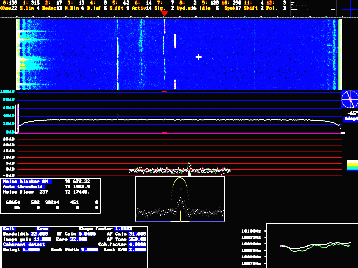
This image of BY1QH calling CQ with DL1MAJ and PA0JMV answering was recorded on Aug 1998. Click here for full size screen image, details of the screen information and samples of audio from the signals on the screen
Typical screen for a good activity weekend (feb 2 1998) and ARRL contest 2000 show how the screen looks under normal usage of dsp.exe. The computer program is presented here as an .EXE file together with the complete source code. The program runs directly under DOS, and uses its own drivers for the sound board and the mouse. The software is written for Watcom C and uses Watcom graphics.
The PC receiver needs some easily built hardware that provides a frequency conversion from signal frequency to audio frequency. With standard building blocks and conventional 10.7MHz filters this should present no problem to the experimenter.
The PC receiver presented here also needs a Pentium MMX computer (or equivalent), a soundblaster 16 (or compatible) and a 1024 x 768 screen with 256 colours.
Some old source code and .EXE files are left with links specifically labeled [OLD INFO]. The old programs may run on old computers with various sound boards and screens, but they are by no means full systems. They are left here mainly as blocks of source code for people wanting to do experiments on older computers by adding their own software ideas. The old .EXE files produce a single channel (mono) spectrum image and an audio output from the loudspeaker.
Hardware and operating system.
The ultimate digital processing
There are three different primary tasks for the PC:A. Remove strong narrowband signals from fellow EME-ers and other strong sine-wave like signals.
B. Remove noise spikes like car ignition noise and power line interference.
C. Dig the desired CW signal out of the remaining (white) noise by use of an adaptive filter (and coherent processing if desired) and send the processed signal to the loudspeaker output. (Optional: Decode the morse dots and dashes and translate into text on the screen.)
The two tasks A and B are difficult to manage simultaneously. Conventionally A is the IF filter and B is the noise blanker. A noise blanker does not work if there is a sine wave like signal present in the passband at levels near or above the level of the noise spikes one wants to remove. This calls for a narrow filter before the noise blanker, but then the noise blanker becomes less efficient because the pulses are stretched by the filter. A conventional noise blanker and filter system is always a compromise although quite good results may be obtained by use of several cascaded noise blankers operating at different bandwidths. For more information about conventional - and some not so conventional - noise blankers look here: Noise blankers
Selective limiters
There is a way around the inherent problem of treating the tasks A and B simultaneously, and that is to use a selective limiter. I have seen (long ago) a description of a wideband selective limiter using proton resonance in paraffine. As I can recall the operating frequency was in the order of 30MHz and the bandwidth about 2MHz. Two orthogonal coils, well balanced from each other, are wound on a block of paraffine. The paraffine is contained in a inhomogenous magnetic field, so for each possible frequency there is an approximate equal amount of protons in resonance. Weak signals can be coupled between the coils by the proton resonance, but as soon as the input signal energy within the natural bandwidth of the proton resonance is above a certain (low) level, the resonanse is saturated, and the output does not go above the saturation level.Weak signals, the wideband noise floor, and all wideband signals like noise spikes are unaffected by a selective limiter. A selective limiter followed by a noise blanker will allow the noise blanker to operate at full performance even with very strong signals present in the pass band.
An optimised receiver based on the standard PC computer has to incorporate a selective limiter in order to allow a well functioning noise blanker within the PC.
Overwiev of the PC DSP software.
Below is a superficial description of the different processing steps of the PC radio software. The links give some more details, but for full information it is necessary to read the actual source code for the various routines.The software is optimised for a dedicated hardware using extreme IF filters at 10.7MHz. The IF filters have a 3dB bandwidth of 20kHz, and they attenuate more than 100 dB outside a 22kHz passband. The software will work with normal IF filtering at correspondingly reduced bandwidth or unwanted signal rejection. The extreme filters put maximum demands on the algorithms and make visible problems that are easily overlooked at more normal bandwidths.
1. Sample the analog data in digital form.
The interrupt routine for the stereo 16 bit A/D conversion contains the first step of data reduction. The real valued data points sampled at 44 kHz in stereo are converted to complex valued data points sampled at 22kHz. Reducing the number of points for the FFT by a factor of two gives a significant reduction of the time required to produce fourier transforms.
2. Convert the input data to overlapping fourier transforms with a bandwidth of about 30Hz.
The complex data at 22kHz sampling rate is converted to fourier transforms using a sine squared window. These transforms overlap and each data point is used twice so this step doubles the number of data points. Together the two first steps provide a spectrum analyser with surprisingly good performance. Look here for further details of the first conversion from the time domain to the frequency domain.
3. Attenuate strong signals selectively and get back to the time domain.
If a strong signal is present, the complex amplitudes produced in step 2 will be too large to fit in 16 bit. Step 3 acts as a selective limiter by attenuating the amplitudes where nessecary so strong signals always fit in 16 bit. Before transforming back to the time domain the total signal is split into two parts. One contains all strong sine wave like signals and the other contains veak signals and wide band noise. For further details, look at Selective limiter and signal split.
4. Detect interference pulses and remove them.
For the time being, only noise pulses are treated. SSB splatter, keying clicks and other interesting problems will be treated in the future (hopefully). The noise blanker locates noise pulses and subtracts a pulse with the correct amplitude, phase/timing and polarisation. For further details, look at The linear noise blanker. The noise blanker needs to know the frequency and phase response of the total filter chain to calculate the expected shape of interference pulses. It is convenient to insert a digital filter that makes the frequency response of the total system extremely flat with accurately linear frequency response. This digital filter is just an array with 1024 complex numbers by which the first fourier transform is multiplied. To "tune" the digital filter automatically the program needs a pulse generator connected to the antenna input. For further details, look at Initialisation of the noise blanker.
5. Make high resolution FFT and locate the signal
The two time functions are added now that impulse noise is subtracted. The summed time function is like the signal that would have been obtained with a selective limiter followed by a noise blanker. The new time function contains less energy at the frequency where the desired signal is located in case some noise pulses were removed. It is used to calculate 8192 point unwindowed fourier transforms by use of the MMX instructions.
The 8192 FFT has a resolution of 2.68Hz. The transforms are used to calculate average power spectra which are used to produce the false colour graph. The routine get_active_signal( ) in ACTIVE.C looks for the strongest signal in the region marked by the operator. By evaluating the correlation between the transforms in the two polarisations coefficients are found that can be used to transform the signal pair that enters the receiver from the two crossed yagis to another signal pair, one with all the signal and the other with noise only.
Once the polarisation is found, the two 8192 transforms can be transformed to two new transforms, one in the polarisation of the signal, the other orthogonal to it. The transformed 8192 transforms (the selected part of them) is the 30dB polarised power spectrum where the green dots show the spectrum ar received with a properly aligned antenna while the red dots show the spectrum as received with an orthogonal antenna. This procedure automatically adapts to any polarisation, linear, circular or elliptic.
The polarisation aligned 2.7Hz power spectrum is used to evaluate the center frequency of the signal as a function of time.
6. Calculate baseband signals using a frequency that follows the selected signal.
The frequency is known from the previous step. It is used to multiply the the summed time function (selective limiter followed by noise blanker) by a sine and a cosine function of the appropriate frequency. As a result all frequencies in the summed time function are shifted by the same amount, causing the desired signal to have zero frequency in the new time function.
Once the desired signal has a frequency very near zero it is trivial to low pass filter and resample at a lower sampling speed. The number of points is reduced by a factor of 32, corresponding to a sampling frequency of 687.5Hz. The resampled signal has a flat frequency response over about 200Hz bandwidth and alias signals due to the resampling are well suppressed.
The resampled signals from the two antennas are transformed by the polarisation coefficients to produce the aligned baseband signal and the orthogonal baseband signal. Both are I/Q pairs and the aligned baseband signal contains the desired signal at frequencies very near zero. In case the signal is drifting with time, the baseband signal has a lower bandwidth than the original signal. The mixing with a "local oscillator" having a similar frequency drift stabilizes the signal frequency and keeps it near zero allowing the use of narrower bandwidth in succeding processing stages.
7. Filter the baseband signals with matched filters.
The baseband signal processing is not time critical because the data rate is low. Floating point arithmetics is used with code written in C.
To locate the signal 1024 point FFT's are calculated using a sine squared window. These transforms have a resolution of about 0.5Hz and thei are calculated with an interleave factor of 4.
The frequency is already stabilised by the digital mixing process of step 6, so normal morse code will be seen as a carrier surrounded by keying sidebands.
In a first step the frequency of the carrier as a function of time is calculated from the power spectra. Once the carrier frequency is approximatively known, it can be determined more precisely from the phase shift from transform to transform.
Once the frequency as a function of time is known for the baseband signal, every second fourier transform is multiplied with the filter function selected by the operator centered at the correct frequency and back transformed. In this way the signal is filtered by a narrow filter with selectable bandwidth and shape factor and centered accurately on the desired signal.
The time function that results from the back transformation is then multiplied with a sine/cosine waveform to shift the frequency of the carrier to zero. In this way errors in the first mixing down to the baseband are compensated. The reason for all the complex processing is that the desired signal may be below the noise most of the time.
The filtering of the aligned baseband signal to a bandwidth of 20Hz or whatever the operator specified produces an accurate function of the frequency as a function of time. Both the aligned and the orthogonal baseband signals are filtered through very narrow filters with only a few Hz bandwidth. Any correlation between these very narrowbanded baseband signals is an indication of errors in the polarisation coefficients and is used to improve them.
8. Send the processed audio to the loudspeakers with or without coherent detect processing.
The previous processing stages have brought the carrier of the baseband signal very close to zero. By filtering through a filter that is "Coh.factor" narrower than the bandwidth 1/t and centered at zero the carrier is recovered. (t is the time for a morse code dot at the CW speed for which the selected filter is optimal)
Once the carrier is known it can be used to determine the phase of the baseband signal. If "Coherent detect" is specified the baseband I/Q pair is transformed so the reference phase is the phase of the carrier which means that the Q component contains noise only and can be neglected. As long as the phase of the carrier is correct the process means that half the noise power is discarded so the S/N will be improved by 3dB. All negative values in the I component can also be neglected since they have to be caused by noise. This will remove half the noise power during "key up" but it will not change anything during "key down" so one might expect another 1.5dB S/N improvement.
In coherent detect mode the I component is used as the amplitude of a tone at a frequency specified by the operator. In normal filter mode the I/Q pair is used to control the amplitude and the frequency of a tone.
To generate the audio signal the FM voice chip of the Soundblaster is used. The amplitude is changed to volume control settings for the Soundblaster internal volume controls in such a way that the dynamic range is expanded. The amplitude and frequency of the loudspeaker signal is updated each time an interrupt is generated for the digital input.
The reason to use the FM voice chip rather than the 8-bit digital I/O was originally to save computer time.
Now that I know the CPU is not the limiting factor I tried to use the 8 bit digital I/O for the output in order to allow SSB and FM reception with some signal processing.
This turned out to be a not so good idea because the isolation between the digital input and the digital output is not good enough so dynamic range was degraded at some frequencies. For the receiving of CW signals the FM voice chip is good enough so it will be retained as the output channel.
The DSP program vers 2.00
To run the program a computer that can handle MMX instructions is required. Pentium MMX at 200MHz and above works fine. What will happen with K6 and other processors is unknown at the present time.The sound board has to be compatible to SB16 and the environment variables have to be set in the usual way with a SET BLASTER= command in the AUTOEXEC.BAT file.
The program needs a SUPER VGA screen and uses 1024x768 pixels with 256 colours. No drive routines have to be loaded, the program has its own drivers for the sound board, mouse and video board.
The program also needs a serial mouse that has to be connected to COM1. (Actually to port address 3F8 with interrupt line 0C) A PS/2 mouse will not work at all.
To run the program, just type DOS4GW DSP at the DOS prompt. When the program is run for the first time the file SIGPROC.INI is created with standard settings for gain, bandwidth and the other processing parameters.
Use C in the main menu to enter receive mode. Dark blue fields indicate areas where things can be changed by a mouse click. Start by clicking at "Init" below "Noise blanker OFF" to initialise the noise blanker. During blanker initialisation a pulse generator has to be connected to both receiver inputs in parallel at a point before any selectivity is introduced.
Download the executable program here: DSP.EXE vers 2.00 (zipped) This .EXE file needs DOS4GW.EXE (zip file) to run in 32 bit mode under DOS. To run the program, you must type: DOS4GW DSP at the dos prompt.
The complete source code DSP200S.ZIP is intended to run in its own subdirectory with the Watcom files under a separate directory \WATCOM directly under the root. If the WATCOM header files are placed elsewhere, DSP.MAK has to be changed.
The files are:
Tha WATCOM directory needs WPP386.EXE, W32RUN.EXE, WLINK.EXE,
WSTUB.EXE WASM.EXE WMAKE.EXE, a subdirectory \LIB for
the libraries (CLIB3R,PLIB3R,MATH387R,EMU387,GRAPH) and a
subdirectory \H, including \H\SYS for the header files.
This is a small sub set of WATCOM, about 4 megabytes.
The bandwidth is roughly the same as in before when a 8192 unwindowed
non-sliding FFT was used but the filter shape is better.
(when a single bin in the FFT is regarded as a filter).
The improved filter characteristics of the longer windowed FFT was
introduced mainly because it allows a more precise determination
of the frequency of very weak signals because of a slightly better S/N.
As a consequence vers 2.02 locks slightly better to extremely weak signals.
The bandwidth of the output is increased so the audio sounds better
for bandwidths above 25Hz.
There are several other minor improvements and the code is simplified,
particularly in active.c.
The algorithms are results of my experimenting and the code becomes
ugly and complex in the first iteration.
Download the executable program here:
DSP.EXE vers 2.02 (zipped)
This .EXE file needs
DOS4GW.EXE (zip file)
to run in 32 bit mode under DOS.
To run the program, you must type: DOS4GW DSP at the dos
prompt.
The complete source code
DSP202S.ZIP
Is structured as vers 2.00 (see above)
The DSP program vers 3.00 is a bit "buggy".
Particularly the signal search function is unstable and it is a
good idea to lock to some spur rather than asking the computer
to find a signal where there is only noise.
To clean up the situation the program would have to be completely
restructured.
I have decided to leave it as it is.
This is the software I currently use for EME and I will continue
to use it until the Linux package has reached an equivalent level.
For normal EME signals there is no significant difference between
vers 3.00 and vers 2.02.
Download the executable program here:
DSP.EXE vers 3.00 (zipped)
This .EXE file needs
DOS4GW.EXE (zip file)
to run in 32 bit mode under DOS.
To run the program, you must type: DOS4GW DSP at the dos
prompt.
The complete source code
DSP300S.ZIP
Is structured as vers 2.00 (see above)
I do not claim any copyright.
The source code is here to encourage particularly radio amateurs
to make their own additions and changes for whatever purpose
of their own.
If you make your own software from the source code here, please
give it a new name of your own - even if you have changed
only a single line. Please, change also the menu text in main.c.
[OLD INFO] The 16 bit version [OLD INFO]
is written for Borland Turbo C (vers 2.0) and Turbo Assembler.
It is included here only as a possible source of inspiration for
amateurs having access to this old compiler, but not to 32 bit
compilers.
[OLD INFO] The 32 bit version (vers 1.00) [OLD INFO]
is written for WATCOM C (vers 11) and WATCOM assembler.
As compared to the 16 bit version, the main difference is speed.
The two programs essentially do the same thing.
[OLD INFO] Vers 1.10 [OLD INFO]
May be used on a 486 computer as long as option C is not
selected.
[OLD INFO] Vers 1.11 [OLD INFO]
This is the last version that can be used without MMX.
A group of .C files.
A group of .ASM files.
GLOBALS.H, ROUTINES.H Header files for C programs.
FOLDCORR.H Header file with butterfly coefficients.
PUBLICS.INC, MAX.INC Header files for ASM programs (global variables)
A.BAT Command to compile and link everything.
G.BAT Command to execute program with DOS4GW
The DSP program vers 2.02
This is a slightly improved version.
The false colour graph is now calculated from a 16384 FFT with a sine
squared window using an interleave factor of 2.
(Each data point is used twice)
The DSP program vers 3.00
This version is not (and will not be) finalised.
Parameters for FFT size (resolution) and AFC (automatic frequency
control) are user selectable.
This version allows detection of extremely weak carriers using a resolution
of only a few tenths of a Hz.
Highly unstable signals can be received at narrow bandwidths because
the AFC can keep the filter centered even for a signal that drifts
quickly.
This version also contains a S/N monitoring mode that is very useful
for tuning the noise figure of receivers.
Liability, Copyright.....
The software on this page is completely my own.
It is presented here to be used by anyone interested on his/her own risk.
I take no responsibility for any damage that may be caused by
malfunction of the software.
Old programs with source code.
Some primitive test programs were placed at this site in 1997.
They are still left here as examples of much simpler code
with more general set up for the Soundblaster board.
Some amateurs find these programs useful for practical EME,
and they may serve as a simple source of inspiration for
people who want to design their own software.