SM 5 BSZ - Practical Design of Very High Gain Yagi Arrays
(July 16 1998)
|
(May 2 2006)
Practical Design of Very High Gain Yagi Arrays.
SM 5 BSZ, Leif Asbrink
1. INTRODUCTION
In a previous article, the "brute force" optimisation method was described.
It is a strategy for antenna optimisation that is convergent,
i.e. the final design is not depending on the initial guess.
If there are too many elements in the initial guess
they disappear by moving into other elements,
and if there are too few elements in the initial design
the local optimum that is obtained is easily detected
by the success when trying to improve gain when adding
one more element somewhere between the others.
In this article tables of various optimum yagi antennas are presented.
These antennas are all calculated with 10 mm element diameter,
and they are designed for a centre frequency of 144.1 MHz.
The antennas are designed for a feed point impedance of 50 ohms,
and for somewhat lower losses than what would produce maximum gain.
The inclusion of impedance and reduced losses is done in a
way described as "nice" antennas in the previous article.
The results of all calculations are given with high accuracy.
This is not because I believe that the accuracy of the model is so high,
it is to allow comparisons between similar antennas,
all calculated in the same way.
I do believe that these differences are accurate to below 0.1dB.
2. DIMENSIONS FOR SINGLE YAGIS
Table 1 gives the theoretical element lengths and table 2 gives
the element positions for a set of yagi antennas,
all optimised for use as a single antenna on 144 MHz.
These antennas form a series of closely related designs,
and I have been using the 9 element version before,
and now I am using the 14 element version.
If these antennas are stacked, they should be stacked at a larger
than usual stacking distance to take advantage
of the very narrow main lobe.
The element positions and element lengths are given in tenths of
millimetres for a design frequency of 144.1MHz.
|
N Refl Rad D1 D2 D3 D4 D5 D6 D7 D8
4 10217 9438 9472 9443
5 10208 9249 9418 9317 9285
6 10198 9169 9403 9305 9119 9188
7 10189 9143 9409 9299 9083 8997 9120
8 10181 9190 9437 9289 9070 8947 8914 9070
9 10168 9325 9492 9274 9066 8928 8855 8853 9031
10 10155 9451 9534 9262 9064 8919 8829 8787 8806 9000
11 10145 9546 9559 9256 9061 8914 8814 8754 8733 8766
12 10135 9623 9575 9254 9059 8910 8805 8734 8694 8688
13 10127 9680 9585 9253 9057 8907 8798 8722 8671 8646
14 10122 9724 9591 9253 9055 8903 8793 8712 8655 8619
15 10117 9755 9595 9253 9053 8901 8788 8705 8644 8601
16 10116 9774 9597 9253 9051 8898 8784 8699 8635 8587
17 10114 9791 9598 9253 9049 8895 8780 8693 8627 8577
18 10113 9804 9599 9253 9048 8892 8777 8689 8621 8568
19 10113 9814 9599 9252 9046 8890 8774 8685 8616 8563
20 10108 9827 9598 9251 9043 8887 8771 8681 8611 8556
N D9 D10 D11 D12 D13 D14 D15 D16 D17 D18
11 8972
12 8733 8948
13 8650 8704 8927
14 8604 8618 8678 8908
15 8575 8569 8589 8655 8890
16 8555 8538 8539 8564 8635 8874
17 8540 8516 8506 8512 8542 8616 8859
18 8529 8500 8482 8477 8488 8522 8599 8846
19 8521 8487 8465 8453 8453 8466 8504 8584 8833
20 8512 8477 8451 8434 8426 8429 8447 8487 8569 8822
|
Table 1. Optimum single yagis.
Theoretical element lengths in tenths of a millimetre for 10 mm
element diameter and centre frequency 144.1 MHz
|
N Rad D1 D2 D3 D4 D5 D6 D7 D8 D9 D10
4 2039 2865 8237
5 2697 3498 9236 16332
6 3252 4114 9662 17481 25135
7 3545 4679 10080 17985 26390 34352
8 3656 5276 10576 18452 27006 35705 43867
9 3766 6027 11328 19079 27657 36533 45412 53718
10 4010 6642 12077 19716 28279 37219 46286 55294 63710
11 4250 7047 12645 20229 28781 37750 46906 56111 65217 73722
12 4473 7341 13077 20647 29194 38182 47388 56691 65997 75178 83758
13 4671 7555 13386 20965 29518 38522 47760 57122 66532 75916 85157
14 4823 7704 13597 21195 29760 38781 48043 57445 66918 76408 85852
15 4945 7814 13743 21362 29943 38977 48265 57694 67210 76761 86314
16 5014 7864 13800 21442 30040 39096 48401 57854 67394 76995 86613
17 5080 7917 13862 21522 30139 39211 48530 58006 67572 77200 86862
18 5130 7951 13896 21575 30206 39293 48627 58114 67703 77357 87046
19 5159 7967 13905 21600 30254 39347 48702 58201 67807 77463 87186
20 5236 8042 13993 21702 30366 39477 48836 58355 67968 77654 87390
N D11 D12 D13 D14 D15 D16 D17 D18
13 93801
14 95146 103842
15 95809 105146 113888
16 96210 105747 115119 123901
17 96524 106168 115738 125141 133958
18 96756 106460 116141 125737 135168 144014
19 96930 106680 116417 126124 135746 145197 154072
20 97157 106941 116725 126494 136222 145871 155346 164244
|
Table 2. Element positions in tenths of a millimetre
for design of table 1.
The performance of the single yagis is shown in table 3.
These antennas work well for the 2 meter dx-er,
providing acceptable SWR between 144.0 and 144.4MHz.
For the beacons above 144.8, the gain is still good,
but the SWR is very high.
For receiving beacons,
with a mast mounted preamp the SWR will have negligible
influence on Rx performance provided the preamp is not oscillating.
If you want an antenna for both satellite and low band work,
choose another design, these antennas have a too low impedance bandwidth.
-------- text added May 2006 ---------
(The pages linked to were previously at the
Antennspecialisten site.)
Besides the unavoidable losses due to the finite conductivity
of the element material there may be additional losses due
to corrosion and due to Eddy currents in the boom tube and
other metallic parts near the element midpoint.
There may also be losses due to dielectric materials,
a small piece of plastic at the element tips may cause
severe losses.
These links may give some idea about the size of this problem.
Losses in elements at 413 MHz.
Losses in elements at 144 MHz.
--------- end of added text -----------
|
N G F/B effic VSWR / Gain loss (dB)
(dBd) (dB) (%) 144.0 144.1 144.3 144.5 144.8
4 7.74 7.3 99.0 1.13/0.00 1.04/0.00 1.21/0.01 1.49/0.02 2.00/0.05
5 9.45 8.6 98.9 1.13/0.00 1.01/0.00 1.30/0.01 1.70/0.03 2.51/0.09
6 10.70 9.7 98.8 1.15/0.00 1.01/0.00 1.37/0.01 1.88/0.04 3.02/0.14
7 11.67 10.6 98.7 1.16/0.00 1.01/0.00 1.42/0.01 2.03/0.05 3.47/0.18
8 12.47 11.3 98.6 1.17/0.01 1.01/0.00 1.45/0.01 2.12/0.05 3.77/0.19
9 13.14 11.6 98.6 1.16/0.01 1.01/0.00 1.44/0.01 2.11/0.05 3.81/0.17
10 13.72 11.9 98.7 1.16/0.01 1.01/0.00 1.43/0.01 2.09/0.04 3.82/0.15
11 14.24 12.2 98.6 1.16/0.01 1.01/0.00 1.42/0.00 2.10/0.04 3.93/0.14
12 14.70 12.5 98.6 1.16/0.01 1.01/0.00 1.43/0.00 2.13/0.04 4.11/0.14
13 15.12 12.8 98.6 1.16/0.01 1.00/0.00 1.43/0.00 2.18/0.04 4.36/0.15
14 15.50 13.2 98.6 1.17/0.01 1.00/0.00 1.45/0.00 2.24/0.04 4.65/0.17
15 15.85 13.5 98.5 1.17/0.01 1.00/0.00 1.46/0.00 2.30/0.05 4.97/0.19
16 16.17 13.9 98.5 1.18/0.02 1.00/0.00 1.48/0.00 2.38/0.05 5.31/0.22
17 16.47 14.3 98.5 1.18/0.02 1.01/0.00 1.49/0.00 2.44/0.05 5.63/0.25
18 16.74 14.7 98.5 1.19/0.02 1.01/0.00 1.50/0.00 2.51/0.06 5.96/0.29
19 17.00 15.0 98.4 1.19/0.02 1.01/0.00 1.52/0.00 2.57/0.07 6.26/0.33
20 17.25 15.3 98.4 1.19/0.02 1.01/0.00 1.53/0.00 2.62/0.08 6.54/0.37
|
Table 3. Performance of yagis, optimised for use as single antennas
3 GOING FROM THEORY TO REAL ANTENNAS.
With the method outlined in the previous article it is easy to
design long Yagi-Uda arrays that produce very good results
according to the computer program with which they are designed.
The theoretical performance of a design with 14 elements
is shown in table 4 and the corresponding dimensions in table 5.
In the design of this array four extra equations were added,
the deviation from 50 ohms, the front to back ratio and the ohmic losses.
All with small weights.
This is the antenna I have been using as a 4x14 cross yagi
array with very good results.
The slightly lower gain compared to table 3 is because of
slightly larger weights on the extra equations and the inclusion
of the front to back ratio.
With conventional high Q designs nearly twice as many
elements are required to produce the same gain, 21.4 dBd.
|
Freq. Gain Impedance F/B Effic.
MHz dBd Re Im dB %
143.6 15.20 31 -6 20.4 99.0
143.7 15.24 33 -4 20.2 98.9
143.8 15.29 35 -2 19.8 98.9
143.9 15.32 39 0 19.3 98.8
144.0 15.36 43 0 18.6 98.8
144.1 15.39 49 1 17.9 98.7
144.2 15.41 56 0 17.1 98.6
144.3 15.43 64 -4 16.3 98.5
144.4 15.44 72 -12 15.5 98.3
144.5 15.44 77 -26 14.7 98.2
144.6 15.44 74 -43 13.9 98.0
|
Table 4. Theoretical gain, impedance,
front to back ratio and efficiency of the 14 element
antenna with dimensions in table 5.
|
Position Theory Experiment
mm Length mm Length mm
0.0 1012.4 1005.5
459.6 974.8 967.8
716.5 960.4 953.4
1260.4 929.8 922.8
2015.4 906.9 899.9
2879.2 891.0 884.0
3751.7 881.2 874.1
4677.7 869.2 862.2
5653.0 856.9 849.9
6641.5 851.8 844.8
7602.0 856.4 849.4
8445.7 866.8 859.8
9456.1 848.6 841.5
10293.3 883.2 876.2
|
Table 5. 14 element design.
Design frequency is 144.1 MHz. Element diameter=10 mm.
Material aluminium.
The experimental lengths are for the elements 14 mm above a
50 mm tube at the centre of each element, at right angle.
If no metal is close to the elements they should be shorted
by about 8 mm more.
This antenna was adjusted according to the procedure in (5) and
the experimental element lengths are given in table 5.
Note that the experimental element lengths are affected by the boom,
made from 50mm tube, and spaced 14mm below each element
(the air gap between boom and element is 14mm).
Using a non conducting boom,
the difference between theory and experiment is slightly larger,
about 15mm at 144MHz.
A measurement of the return loss a function of frequency
shows that the impedance is very close to 50 ohms at the
design frequency for the experimental antenna after the
adjustment procedure.
The variation of SWR and side lobe level with frequency also
agree very well between theory and experiment.
Note that the adjustment procedure in (5) uses only the radiation pattern.
This observation leads to the following complete design procedure,
which also has been verified experimentally:
|
|
a) Make the theoretical design,
or get it from this article or any other source.
The steps below assume the design to have a theoretical impedance
of 50 ohms resistive.
If you like some other impedance better,
the necessary changes are obvious.
b) Build an experimental array, on a non conducting boom.
Make sure to keep it well away from conductors.
Use a properly designed 1:1 balun to connect the feeder to the antenna.
In my experience ferrite baluns are not good enough.
Verify the balun with a 50 ohm resistor,
the SWR should be very close to 1.00.
Measure the attenuation when a signal is transmitted through the balun,
still loaded by the 50 ohm resistor,
with one side of the resistor connected to the level meter
and the other unconnected, fig 1.
The attenuation should be 30 dB or more regardless of
which side is left open.
The SWR has to remain 1:1.00.
A good balun is easily made by an electrical l/4
wavelength sleeve, fig1b.
c) Find out at what frequency the impedance as a function
of frequency is similar to the theoretical curve
and calculate the relative frequency error
dF = (Fexp-Ftheory) / Ftheory
If dF is small enough this step is finished.
d) Adjust all elements by equal amounts dL= 1.3 * wavelength * dF.
Repeat c and d. 2 or 3 iterations should be enough.
If you are happy with an antenna on a non conducting boom, this is all.
e) Mount the reflector and all directors except the one nearest
to the radiator at the centre of 0.1 wavelength pieces of the boom you
want to use with exactly the same mounting method you want to
use for the final antenna.
All these N-2 pieces have to be made from one tube dimension.
If the element is mounted through the boom the inner diameter as
well as the outer diameter have to be the same for all elements.
If you want to use a boom that is thicker at the centre,
repeat the steps e to h for all different boom dimensions, one at a time.
f) Repeat steps c and d for the design of step e,
but adjust only the N-2 elements that are mounted on metal,
leaving the radiator and the director very close to the radiator unchanged.
They are already correct for their mounting on a non conducting boom.
When the partly metal mounted antenna is at the right frequency,
you have found out exactly which correction was needed to
compensate for the boom of your choice,
with the element mounting method of your choice.
g) Apply the length compensation from step f to the first director,
and mount it and the radiator on a piece of the boom tube, long enough
to stick out at least 0.05 wavelengths outside the two elements.
D1 should of course be mounted exactly the same way as the other directors,
but the radiator may be mounted differently.
If the directors and the reflector are mounted through the boom
it is convenient to mount the radiator on top of the boom,
for example on a square piece of 3mm thick polypropylene.
Moving the radiator slightly away from the straight line connecting
the centre point of the other elements does not change the
radiation properties of the antenna much,
particularly if the radiator is designed to have a high impedance,
and hence low currents, as the designs in this article.
h) Adjust the length of the radiator for SWR=1 on the design frequency.
The radiator is differently affected by the boom,
and a different correction is needed for it.
i) If you do not want the boom tube to stick out about 0.05
wavelengths at the ends, cut the boom tube piece as close as
mechanically possible in front of the last director.
If the SWR changes, lengthen the last director until the
SWR is back at its old value.
For this step, check SWR at several frequencies.
If you want a cross yagi, you need some extra boom behind the reflector
to support the feeders that preferably are brought out backwards.
Otherwise you can cut the boom as at the other end,
and use the same correction to the reflector.
|
|
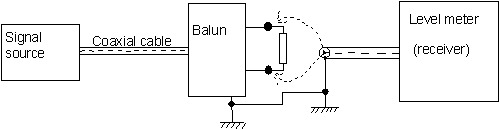 > >
Figure 1. Checking a balun. The resistor should match the balun
output impedance (to give SWR = 1 at the signal source).
The ground point on the cable between the signal source
and the balun should be a point near to the two balanced output
terminals of the balun.
The level meter is connected first to the upper end of the resistor,
and then to the lower end as indicated by the dotted arrows.
In both cases a very low reading should be observed.
Use very short leads and be careful to avoid stray capacitances.
When the other end of the resistor is connected to ground,
the signal level should go up by 30 dB or so.
The ground point for the balun is any point of the outside metal cover
or the outside of the cable between the signal source and the balun.

Figure 1a. Any sleeve is a good balun at some frequency as long
as it is not containing bad plastic like PVC.
In this figure the PVC of the coaxial cable is covered by
a thin tube to which the outer conductor of the
cable is connected at the right (antenna) side.
At the other end, this tube is connected to the
outer sleeve.
It does not matter if the cable outer conductor is connected
or not here, there is no current on the outside.
If the cable is covered by polyethylene, or if the plastic
cover is removed from the cable, the inner tube is not needed.
Then the outer sleeve is just connected to the blank outer
conductor of the coaxial cable at the left (station) side.
The outer sleeve has to be kept in place with some spacers.
It is also possible to make the balun from thick coaxial
cable in which the inner conductor is hollow.
The inner conductor may be left in space, or removed.
As seen from the antenna side, the balun is a shorted
1/4 wavelength cable with the outer sleeve as the outer
conductor and the cable screen (or inner tube) as inner
conductor.
No current will flow from the cable screen to the outside
of the sleeve because of the high impedance of a
shorted quarter wave section.
The problem is to know what the real velocity factor is.
Practically one makes a guess on the proper length.
Manufactures a balun, and then measures at what frequency
it works properly.
When length and frequency is known it is easy to calculate the
velocity factor and make a new balun that will be very close
to the correct frequency.
A small airgap (low characteristic impedance) causes
narrow bandwidth.
If very short teflon spacers are used, the wave speed is
speed of light, but if a foam dielectric fills all of
the balun (made from foam filled cable) the wave speed is
close to specifications for that particular cable.
The frequency can be adjusted by squeezing the outer conductor.
Squeezing at the antenna end lowers the frequency.
Squeezing at the station end increases the frequency.
(Think of it as increasing C respectively lowering L in a LC resonance
circuit. C is where the electric field is and L where the magnetic.)
The procedure described above may seem difficult and time consuming.
It is not really so, the process is rapidly convergent
and should not require many hours.
The reason for this process is that boom corrections available
in the amateur literature are seriously incorrect,
and for optimised yagis like the ones in this article they are
not good enough.
For example, it is not generally known that the wall thickness
of the boom tube, as well as the hole diameter and the element
diameter affect the element correction for elements mounted
through holes in the boom.
To get a feeling for the physical reason for the boom correction,
consider the centre part of an insulated element passing through
a hole in the boom.
The dominating effect of the boom is that it lowers the inductance
of the element inside the boom.
The general inductance formula is an integral of the square of
the magnetic field.
The currents flowing on the inside of the boom reduces this integral,
in the extreme case of the boom being a solid rod,
with a hole in it allowing only a very thin insulator,
all the way down to zero.
In the latter case the effect of the boom is the same as
for a non insulated element.
From this argument it should be clear that the hole size as
well as the wall thickness are important.
-------- text added May 2006 ---------
(The pages linked to were previously at the
Antennspecialisten site.)
The practical procedure outlined above is not as important
now as it was in 1998 when this article was written.
Here are links to some more recent information that can be
used to evaluate what boom correction to apply when isolated
elements are mounted through holes in the boom tube.
General discussion about boom corrections.
BC, a PC program for boom corrections.
Boom corrections from other sources
Previous work by others.
Experimental setup
for measurement of boom corrections in a cavity.
Details
Evaluation of boom corrections from cavity measurements.
-------- end of added text ---------
4 DESIGN OF ARRAYS OF YAGI ANTENNAS.
When stacking the antennas designed for use as single yagis,
the calculated performance is typically as illustrated for
the 9 and 14 element cases in fig 2.
The figure shows performance for stacking 4 antennas with
identical stacking distance in E and H planes.
For 14 elements a stacking gain of 6.15 dB is obtained
at a stacking distance of 6.2 meters.
With this large stacking distance the main lobe is very sharp,
but the side lobes are very strong and most (or all)
amateurs would prefer a shorter stacking distance to reduce the side lobes.

Figure 2. Variation with stacking distance of gain and
standing wave ratio for symmetric stacking of 4 yagi antennas.
These yagis are optimised for maximum gain as single antennas,
and VSWR is with respect to the nominal 50 ohm impedance that these
antennas have as single antennas.
The gain figures assume proper matching to the actual feed
point impedance (as should always be the case when narrow band antennas
are specified)
To illustrate the effects of stacking,
fig 3 shows the total amount of power radiated from
the forward direction up to a certain angle as a function of that angle.
In figure 3 the 14 element design in tables 1 and 2 is shown as a
single antenna, curve A.
Four of the same antenna stacked at 6.5 and at 4.5 meters is curve
B and C respectively.
For this 14 element design about 10% of the power is
radiated at angles above 50 degrees regardless of the stacking distance.
Stacking at 6.5 meters only affects the radiation between
0 and 12 degrees - above 12 degrees the wide spaced
array radiates as a single antenna.
Stacking at 4.5 meters obviously makes the main lobe
wider (by approximately 6.5/4.5) but the side lobes
due to stacking disappear, and even the side lobe of the
single antenna at 28 degrees is a little attenuated.
Stacking the 14 element antenna at 4.5 meters gives a
stacking gain of only 5.6 dB.
Although quite conventional, this way of stacking is poor
use of the potentials of the yagi array.
By repeating the optimisation process,
this time with all the 56 elements of four yagis stacked
at 4.5 meters a new design optimised for stacking
at 4.5 meters is obtained.
This re-optimised antenna has slightly higher gain,
which is fine of course, but the important advantage
of reoptimization is that the improved gain comes
only from reducing radiation in spurious lobes without
any change in the shape of the main lobe.
As a result the re-optimised antenna has only about 5%
of the radiated power above 50 degrees which is a
reduction by a factor of two by the reoptimization process.

Figure 3. Percentage of power radiated in the angle interval 0 to
v degrees from the main lobe for 14 element yagis.
When v = 180 degrees, all directions are included and
100% is obtained for all antennas.
The conventional definition of G/T assumes that any sensitivity
below v=30 is harmless, while at v > 30 degrees the antenna will
start to see noise sources.
A = Single 14 element antenna. Optimised as single.
B = 4 x 14 element stacked at 6.5 x 6.5 meter. Optimised as single.
C = 4 x 14 element stacked at 4.5 x 4.5 meter. Optimised as single.
D = 4 x 14 element stacked at 4.5 x 4.5 meter. Optimised
for stacking at 4.5 meter.
The antenna designed for stacking at 4.5 meters has a cleaner
pattern than the one designed for use as a single antenna,
and is more suitable as a candidate for a commercial product.
If you plan to use a single antenna only,
a small loss in forward gain is not a big issue.
If you want to use many antennas in a stacking arrangement,
the clean pattern is extremely valuable,
and it is difficult to use very large stacking distances
for mechanical reasons, so the very sharp main lobe of the
antenna optimised as single is wasted anyway.
To further illustrate what is possible to obtain when
stacking 4 yagis of about 5 wavelengths,
a set of designs is presented in table 6 and 7,
their performance in table 8.
|
Dist Refl Rad D1 D2 D3 D4 D5 D6 D7
1.5 10119 9543 9649 9100 8658 8506 8547 8455 8104
2.0 10123 9760 9659 9323 9026 8611 8175 8104 8333
2.5 10154 9841 9609 9310 9126 8979 8854 8755 8681
3.0 10175 9895 9644 9346 9180 9059 8949 8834 8709
3.5 10145 9872 9650 9328 9153 9019 8908 8807 8705
4.0 10080 9816 9667 9289 9107 8972 8861 8755 8683
4.5 10140 9819 9637 9293 9069 8910 8831 8760 8658
5.0 10166 9788 9585 9289 9063 8885 8767 8690 8628
5.5 10212 9713 9574 9267 9069 8873 8703 8620 8613
6.0 10106 9684 9598 9231 9048 8886 8716 8592 8630
6.5 10133 9694 9581 9235 9015 8873 8788 8716 8655
Dist D8 D9 D10 D11 D12
1.5 7640 7635 8233 8819 8853
2.0 8557 8719 8779 8713 8544
2.5 8626 8578 8526 8470 8547
3.0 8578 8448 8331 8225 8418
3.5 8600 8497 8377 8274 8603
4.0 8619 8515 8444 8569 8681
4.5 8551 8534 8617 8708 8726
5.0 8598 8617 8683 8635 8884
5.5 8643 8705 8685 8570 9013
6.0 8688 8655 8592 8760 8950
6.5 8594 8571 8647 8775 8923
|
Table 6. Optimum 14 element yagis for stacking.
Theoretical element lengths in tenths of a millimetre
for 10 mm element diameter and centre frequency 144.1 MHz
|
Dist Rad D1 D2 D3 D4 D5 D6 D7 D8 D9 D10
1.5 4610 6992 12169 20066 29581 38500 47353 56984 67276 77412 86385
2.0 4710 7152 12486 19462 28097 38183 48711 58624 67509 75986 84847
2.5 4786 7684 13768 21277 29424 37937 46745 55841 65209 74800 84534
3.0 5029 7710 13464 20671 28617 36995 45773 54928 64374 74030 83768
3.5 5104 7626 13114 20428 28525 37196 46132 55317 64717 74180 83862
4.0 5400 7774 13085 20569 28997 37669 46903 56238 65482 75095 84867
4.5 4889 7399 12867 20193 29026 38047 46968 56252 66054 75840 84871
5.0 4789 7563 13331 20622 29228 38429 47829 57353 66906 76208 85208
5.5 4915 7806 13564 21034 29284 38857 48535 58208 67684 76422 85808
6.0 4827 7528 13071 20911 29457 38323 48452 58199 66956 76387 86216
6.5 4683 7477 13235 20874 29977 39070 47905 57151 67001 76903 86028
Dist D8 D9 D10 D11 D12
1.5 67276 77412 86385 94883 104069
2.0 67509 75986 84847 94168 103330
2.5 65209 74800 84534 94302 103289
3.0 64374 74030 83768 93612 102363
3.5 64717 74180 83862 93603 102106
4.0 65482 75095 84867 93827 102567
4.5 66054 75840 84871 93812 102593
5.0 66906 76208 85208 94748 103167
5.5 67687 76422 85808 95404 103778
6.0 66956 76387 86216 94961 103657
6.5 67001 76903 86028 95037 103789
|
Table 7. Element positions in tenths of a millimetre for
the design of table 6.
|
Dist G F/B Effic. G loss Power 0 to Single ant
145.1 x degrees (%) Z G
(m) (dBd) (dB) (%) (dB) x=10 x=20 x=30 x=50 (ohms) (dBd)
- 15.50 13.2 98.6 0.36 37.9 77.0 80.8 90.0 50.0 +i0.1 15.50
1.5 17.63 13.2 98.9 0.20 53.3 83.2 88.9 91.9 21.5,-i29.0 13.21
2.0 18.33 14.7 98.8 0.16 59.5 86.6 90.5 92.9 24.3,-i18.5 14.12
2.5 18.76 16.7 98.4 0.20 62.0 85.8 86.4 93.1 20.0,-i2.1 15.24
3.0 19.38 24.8 98.4 0.18 69.0 92.5 92.8 96.5 33.6,+i1.4 15.06
3.5 20.17 27.7 98.6 0.25 75.6 92.9 93.9 97.0 41.4,+i0.5 15.17
4.0 20.79 25.0 98.7 0.33 77.5 89.3 91.9 96.0 43.1,+i1.1 15.33
4.5 21.20 20.7 98.7 0.35 74.3 84.7 88.8 94.4 46.9,+i3.1 15.41
5.0 21.44 17.2 98.7 0.33 67.8 80.8 85.7 92.3 48.9,+i3.5 15.44
5.5 21.61 15.2 98.7 0.37 60.6 78.8 83.9 91.4 50.6,+i4.0 15.43
6.0 21.67 14.0 98.7 0.40 52.8 77.1 82.4 90.6 52.2,+i3.0 15.44
6.5 21.65 12.7 98.6 0.50 45.4 75.2 80.0 89.0 52.9,+i0.6 15.46
|
Table 8. Performance of 4x14 element at different stacking distances.
Antennas of tables 6 and 7 at the stacking distance they are designed for.
The first row is for a single antenna, the design of table 1 and 2.
If you want an antenna for EME only, and you live in a quiet environment,
like I do, a good antenna would be 4x14 stacked at 5.0 or 5.5 meters.
If you are interested in IONO-scatter and meteor scatter as well,
4.5 meters would be a better choice, because for scatter you want
to maximise the power close to the main lobe,
and at 4.5 meters 75% is within +/-10 degrees while the gain
loss is only 0.47dB from the maximum at 6 meters
(with only 50% within 10 degrees).
If you live in a densely populated area with a lot of man made noise,
and TVI is a problem the optimum stacking distance would be 3.5 meters,
giving 93% of the power within +/- 20 degrees and a gain of 20.17 dBd
which is still a good gain figure for EME.
Note that stacking of the antenna designed for use as
a single antenna at this short stacking distance gives only 19.67dB,
and that the gain loss comes from undesired radiation in side lobes
with only 76% of the power within +/-20 degrees.
If your station performance is limited by QRM or TVI,
the reoptimization for stacking is a 6dB improvement at 3.5
meters stacking distance !!!!
This should be a memento to everybody planning to get a clean
pattern from understacking yagis(not designed for it).
From the discussion above it should be clear that the optimum
antenna is not necessarily the one with maximum gain.
As a single figure of merit G/T (gain divided by noise temperature)
has become popular.
For 144MHz however this quantity is quite arbitrary since it depends
on the assumption that man made noise can be treated as an elevated
ground temperature, 1000 degrees Kelvin or so.
Although G/T is closely related to G/(fraction of power
radiated above 30 degrees), I think the proper choice of
antenna is best made by considering more than a single figure of merit,
at least on 144MHz.
The integrated radiation from the forward direction up to a fixed angle,
for several fixed angles is easily calculated,
and these numbers should be considered together with gain and ohmic losses.
To find the proper correction for the systematic errors,
and for the influence of the boom on a close spaced stacking
configurations is possible.
One way is to evaluate all corrections on a design,
optimised for use as single,
then using the same corrections for the antenna designed for stacking.
The other alternative is to use capacitors and resistors in series
or parallel to change the impedance of a single antenna to 50 ohms,
then the corrections can be evaluated as above.
(For 14 elements at 3.5 meters,
connect 2x4.7 ohm resistors in series with the antenna,
one at each side).
A network analyser that gives the impedance directly would of
course be perfect.
5 SOME DIFFERENT OPTIMISATIONS.
Up to this point the results presented is for maximum gain
with a certain number of elements,
with the requirement of 50 ohm feed point impedance.
If the first director is removed,
the feed point impedance will fall to low and unpleasant values but t
he gain is reduced only with a small number,
so such designs give a higher gain per element and a slightly
lower gain per boom length.
Inserting more elements on the same boom length will after
reoptimization give a very small improvement (in the order of 0.01dB),
not worth the extra element(s), if the element(s) is inserted on one
or the other, or both sides of the radiator.
More elements between the directors remove themselves in the
optimisation process.
Of course I have not tried all possibilities,
but all start designs with more elements I have tried end up in
the designs above.
A systematic study of gain for symmetric arrays of 4 yagis optimised
for different stacking distances produces too much data to be published
here.
The performance of the antennas of such a study is shown in table 9
and fig 4.
When calculating the gain for a symmetric array of 16 small
yagis as a function of stacking distance one finds a maximum
at about 3.7 or 3.8 meters.
This maximum originates in the array factor,
the pattern produced when stacking isotropic radiators.
Optimising antennas for use in a 16 yagi array for the
stacking distance of this peak gives the performance
illustrated in table 10 and fig 5.
For the larger designs the maximum disappears and these antennas
are optimised for 3.8 meters.
There is a second maximum originating in the array
factor at about 5.7 meters,
but antennas suitable for stacking at such a large distance
have too many elements to be practical to study with my computing resources.
6 INFLUENCE OF METAL NEAR THE ANTENNAS.
For a single yagi there is no need to have any metal that will
interact with the electrical field near the antenna.
All metal parts near the symmetry plane of the antenna
(the plane that cuts each element in two equal parts) are harmless
from an electric field point of view.
Of course tubes or sheet metal in or near the symmetry plane
will still affect element lengths exactly as the boom tube does
if they come very close to the elements, but this can easily be avoided.
For a stacking arrangement of 4 horizontal yagis,
the centre part of the conventional H structure is far away
at normal stacking distances, and the influence is small.
For larger arrays of horizontal yagis, long horizontal metal
structures are normally used.
They are spaced at half the stacking distance from each antenna,
and they may influence the gain slightly.
I have tried to simulate the effect of these by surrounding
an antenna by the metal needed for stacking in a large structure at 4 m
stacking distance (both the horizontal and vertical parts -
they interact) the effect on gain depends on the positioning
of the yagi along the boom, and the result of this simulation
is given in fig 6.
Increasing the size of the model stacking harness
does not change the general pattern,
so it is not caused by any sharp resonance in the long tubes.
It is not easy to judge if this simulation gives a realistic
estimate of what to expect in the real world.
It would be interesting to see calculations on influence of
surroundings calculated with different computer programs.
In any case it seems to be reasonably safe to use metal
constructions in the conventional way also for stacking highly
optimised horizontally polarised yagis.
Cross yagis are of course more difficult.
In my design (photo?) the booms are from aluminium,
but the support structure up to 0.8m away is made from plastic
tubes (with glass fibres) and the feeders leave the antennas well
behind the reflectors.
Model calculations however indicate that metal
tubes straight through the antennas are nearly harmless if the point
where the tube passes through the antenna is properly selected.
The calculation assumes that the boom is not conducting,
but adding a conducting boom does not cause any dramatic differences.
I am not sure this model calculation is really showing the
true influence of metal in the strong electric field near the antenna.
On the contrary my experience from measuring the far field while moving
a long tube in the positions corresponding to the model
calculation made me choose the design with plastic tubes.
To SM 5 BSZ Main Page
|
 >
>


