This article has been published in DUBUS 2/2004 and it is protected by copyright. Any reproduction, publishing in the Internet or commercial use only with the written permission from the publisher Verlag Joachim Kraft DUBUS Web page

This article has also been published in CQ VHF in two parts, Spring 2005 and Summer 2005.

Transmitter Testing

Leif Asbrink, SM5BSZ

 http://www.sm5bsz.com/index.htm



The importance of a good dynamic range in receivers is well known among amateurs. Receiver dynamic range seems to be one of the important factors behind commercial success or failure for a transceiver model. The quality of the transmitter is of course equally important, but transmitter testing does not get the same attention in amateur publications, and methods for transmitter testing are far less satisfactory than currently used methods for receiver testing. There is an obvious reason of course. The deficiencies in transmitter design that cause unnecessary interference do not create problems to the owner! It is other people – his neighbours on the bands – who suffer from the QRM. It is certainly meaningful to try to improve the standards of amateur transmitters because today the transmitters are usually the limiting factors, particularly on VHF.

In the previous article of this series [1] the quantity DR2 was introduced for the two-signal dynamic range of a receiver. The way it is defined, in 1 Hz bandwidth and with 3 dB degradation of the S/N of the weak signal, makes DR2 equivalent to transmitter sideband noise. To understand this concept, imagine a receiver that has DR2 = 133 dBHz which is what is required on 7 MHz according to [2]; and also imagine a transmitter with a sideband noise level of –133 dBc/Hz. Using that receiver, a strong signal from a perfect transmitter will cause a certain amount of S/N degradation of a weak signal. Assuming the same signal levels for the strong and weak signals, the sideband noise from the noisy transmitter will cause exactly the same S/N degradation to a weak signal in a perfect receiver.

A DR2 dynamic range of 133 dBHz may be adequate on HF bands, but the situation on VHF is very different. For this dynamic range to be adequate when two 100W stations on 144MHz are beaming towards each other, the stations would need to be separated by as much as 100km! So it is not uncommon for the VHF amateur to find DR2 and/or transmitter sideband noise is the limiting factors when trying to work DX. For a typical VHF rig, DR2 is actually worse than in this example, only between 110 and 120 dBHz at a frequency separation of 20 kHz. Transmitters are often worse than receivers, even when transmitting an unmodulated carrier.

There is also some confusion about the meaning of the word “test” when it comes to transmitter testing. In a factory one should have a pass/fail test; something that is well defined and produces the same result on the production line as it does in the laboratory. The purpose is simply to find faulty units to make sure they do not reach the market. But when a transmitter is being tested for a product review, the meaning of “test” is something entirely different, then one wants a test that reveals all out-of-channel emissions that the test object may produce in real life when operated within the recommendations of the operating manual. Tests done by development engineers are yet another thing. In the development phase one uses a large range of very specific tests on individual building blocks to optimise them separately. Interference can be generated by many different mechanisms, and it is the responsibility of both the development engineer and the review engineer to seek these problems out, using whatever tests are needed to reveal them. While the pass/fail test has only two outcomes, yes or no, the output from product review testing is a lot of data that should inform the prospective buyer whether the unit in question is suitable for his intended usage.

As I see it, the only honest procedure to test the purity of a transmitter’s signal for a product review can be described in words like this: “Connect the transmitter to a spectrum analyser, and operate it as described in the operators manual while watching the spectrum. Vary the modulation with pauses and different voice levels for SSB. Observe what happens when the VOX, QSK or PTT button switches between RX and TX. Note spurious emissions that happen infrequently, and adapt your input to the transmitter to try to make them happen often and repeatably. In general, operate the transmitter to create the worst-case interference within the limits given by the operators manual.” The output of such a test is the worst case spectrum and a description of the worst case modulation input.

One of the main problems in modern transmitters is the ALC, a servo system that is designed to keep the output power below a certain threshold. Any servo system can have stability problems and the ALC system of a transmitter is no exception. The interference generated can be horrible – but a standardized two-tone test will not show anything at all. It is becoming well known that the simple two-tone test does not reveal much of the real performance of a SSB transmitter. With two constant tones that are separated by 1 kHz, exactly the same maximum power is reached 1000 times each second. With the fast attack, slow release ALC characteristic of a typical SSB transceiver, the ALC control voltage will be very close to a DC voltage with just a small saw-tooth like component superimposed on it. Likewise the power supplies will be operating under nearly constant load, and their dynamic regulation is not being tested at all. Consequently the two-tone test will not show many of the problems that may occur during normal usage with voice modulation. It only shows the fundamental linearity of the final amplifier, not the rig as a whole.

The simple test, just measure the emitted spectrum while modulating the transmitter as if it was on the air, has a practical problem: professional spectrum analysers are not good enough! The sideband noise levels of the oscillators in the spectrum analyser (a multiple-conversion superhet) need to be substantially lower than those in the transmitter under test, or else you are measuring the test equipment, not the transmitter. The ones I have access to have sideband noise levels of about –100 dBc/Hz at 20 kHz, and the best performance I know of in a commercial instrument is –125 dBc/Hz at a frequency separation of 10 kHz (Rohde & Schwarz FSU series). This problem arises from the need to make professional test equipment broadband from near-DC to perhaps several GHz; but for testing amateur equipment we do not need broadband coverage, and therefore high-quality measurements are not so difficult, as will be shown below.

There is another problem, however, a more fundamental one that requires some discussion. The interference caused by a transmitter, be it noise sidebands, splatter or keying clicks, occupies a large bandwidth. The level one will see on a spectrum analyser depends strongly on the bandwidth, the sweep speed and the detector used. To produce a good characterisation of the interference it will be necessary to make two measurements – one that uses a peak-hold detector in SSB bandwidth and another that uses a detector for the average power in a narrow bandwidth. The two measurements are discussed in detail below.

The average power spectrum

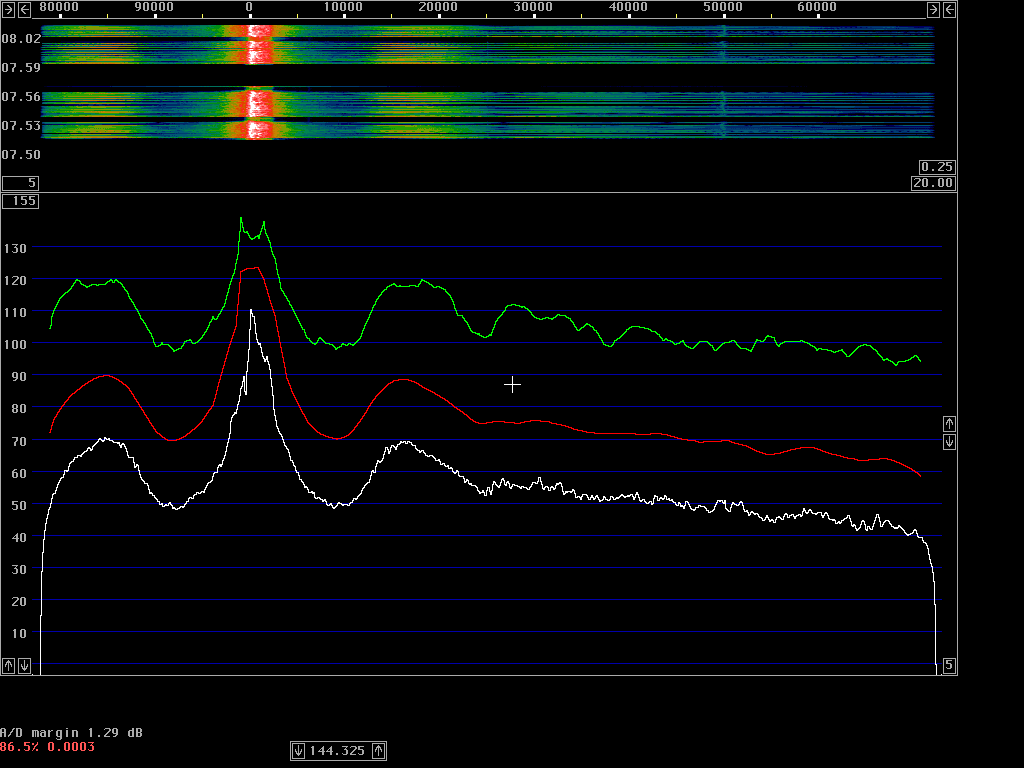
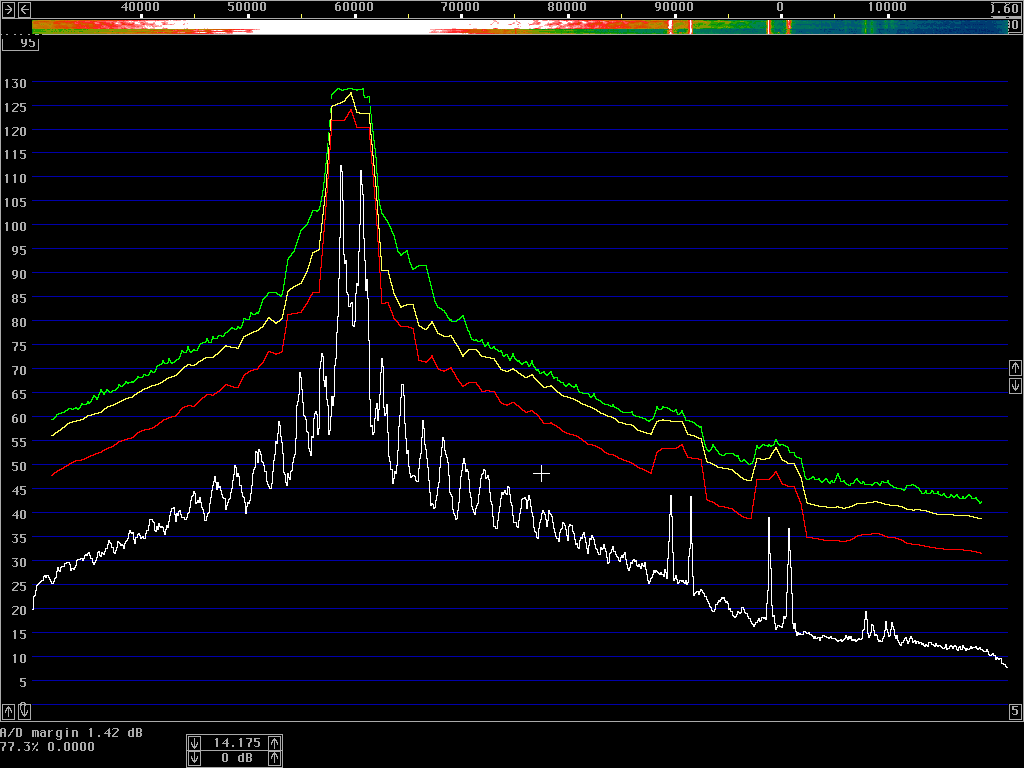
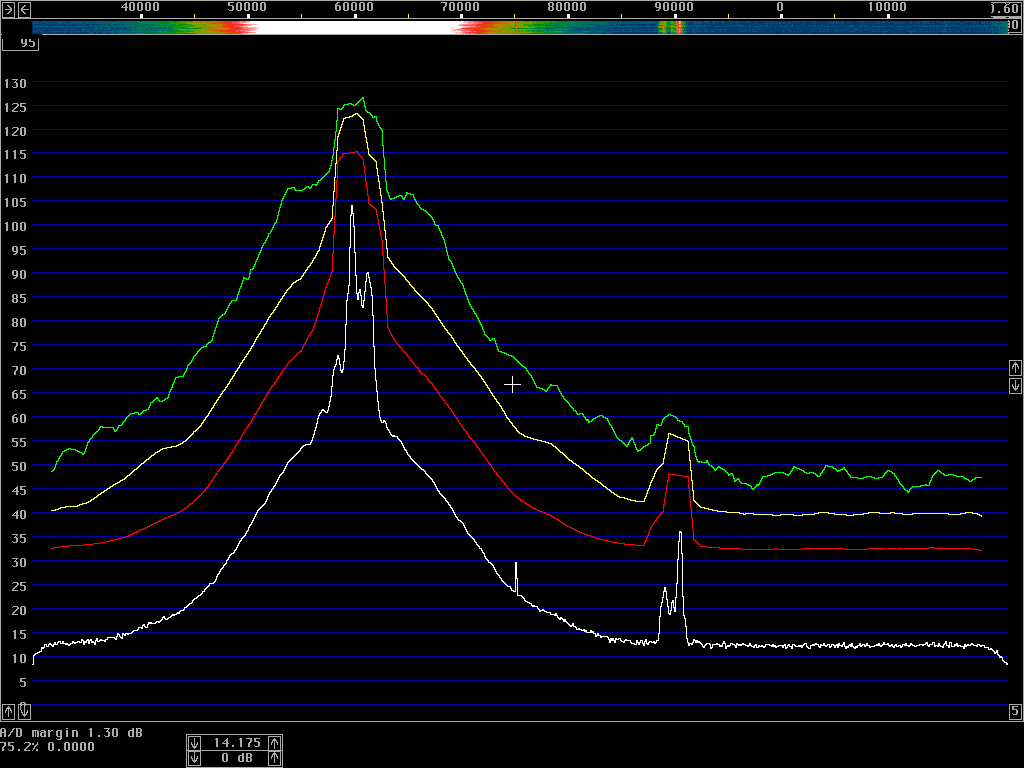
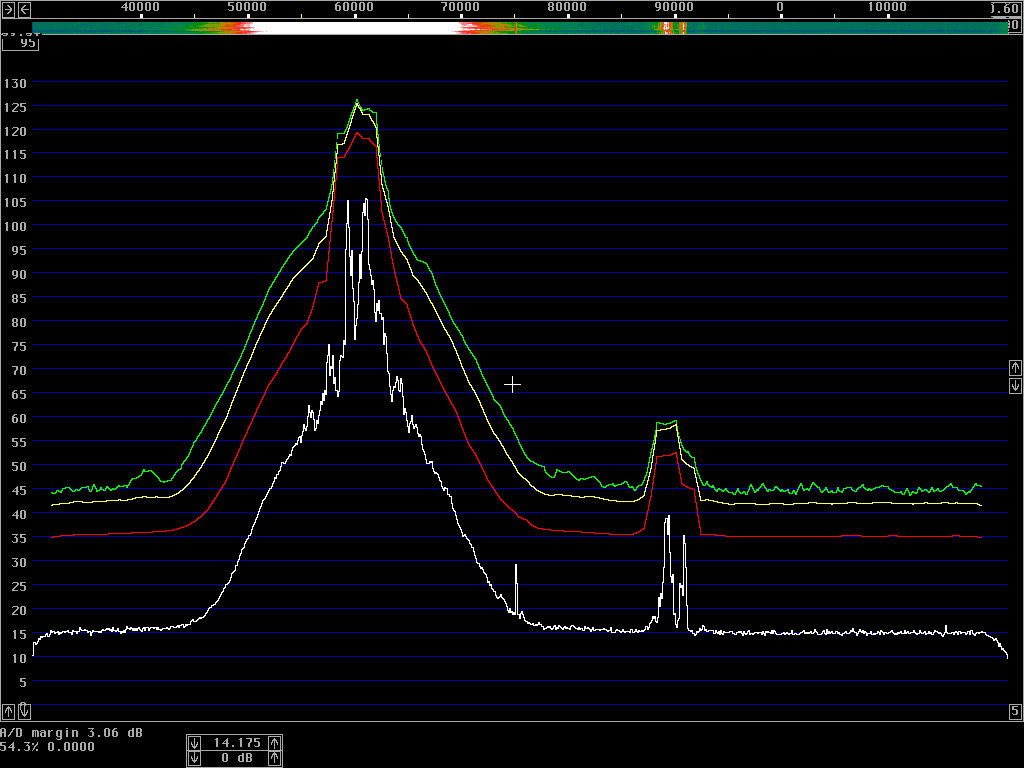
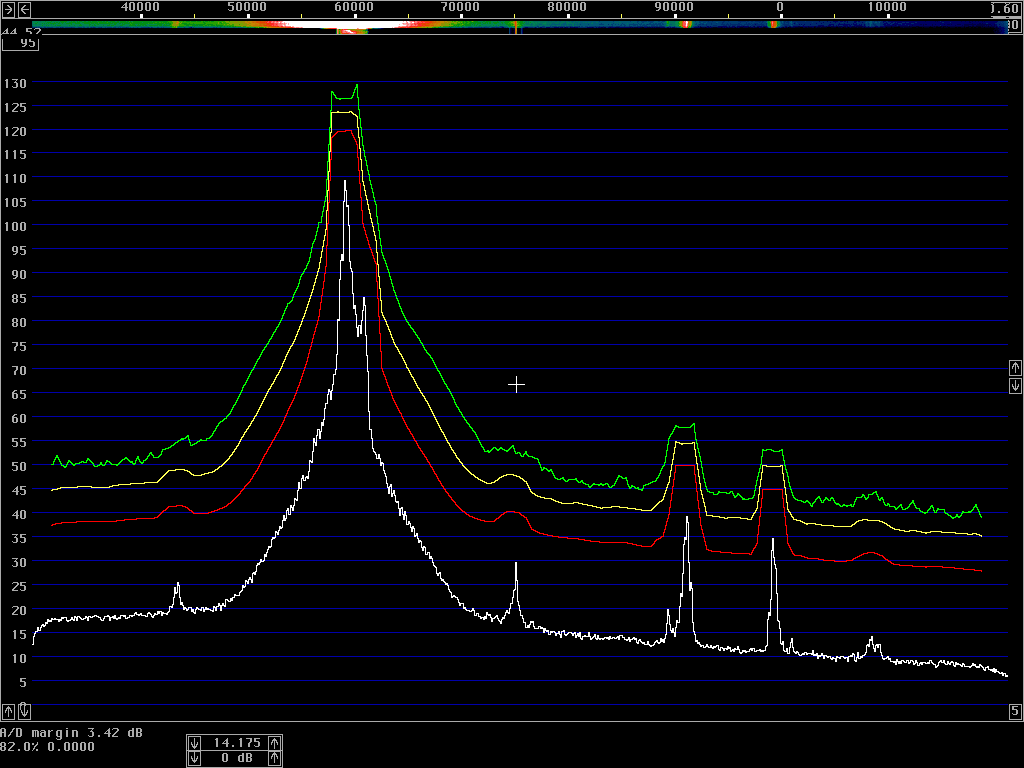
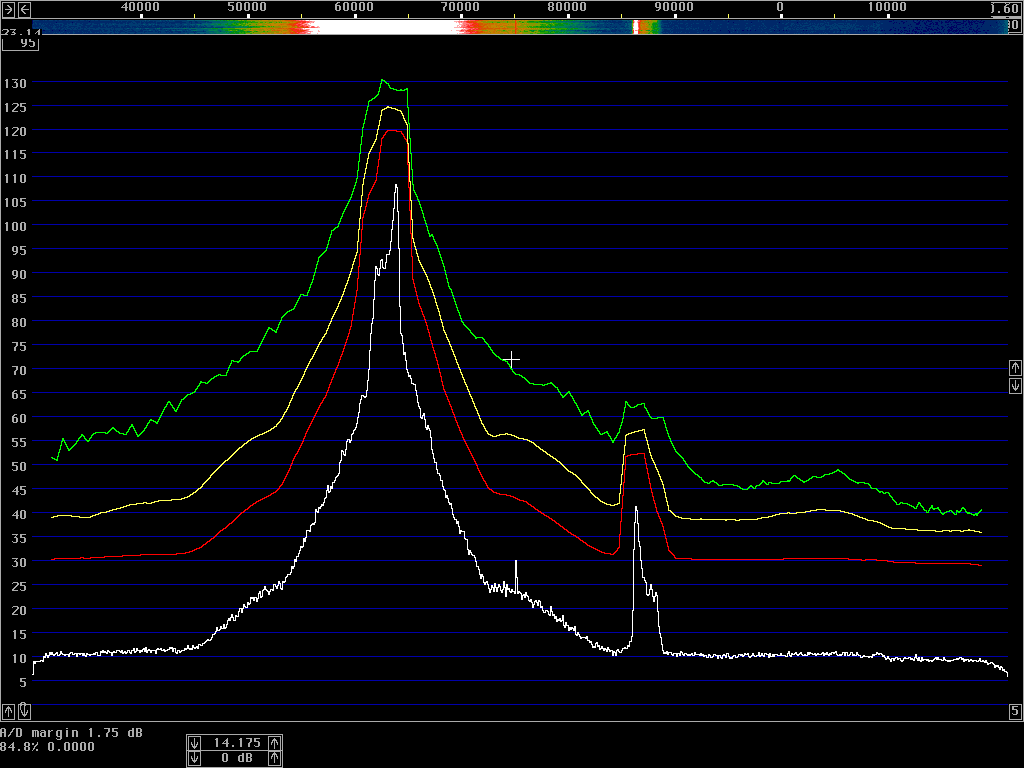
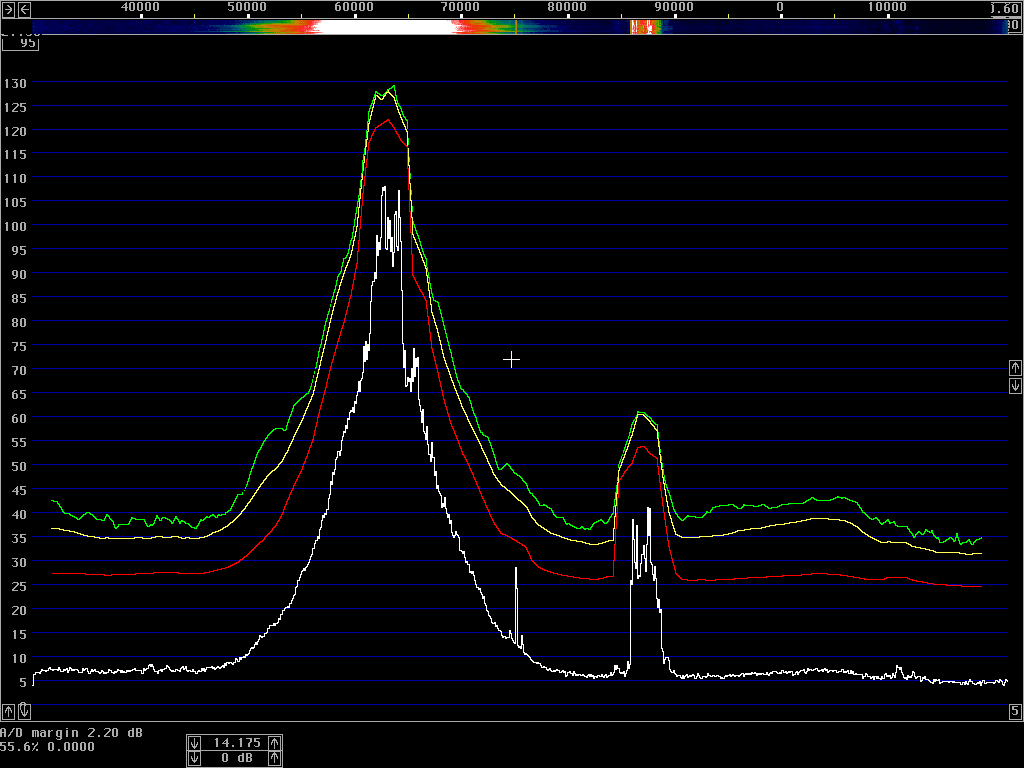
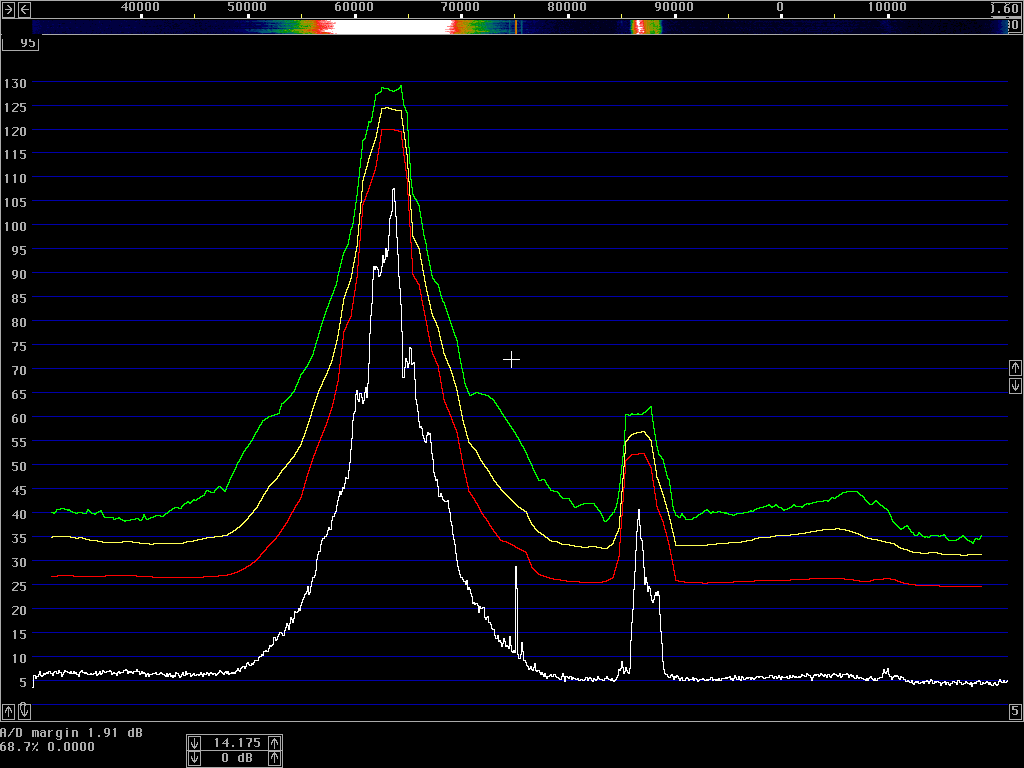
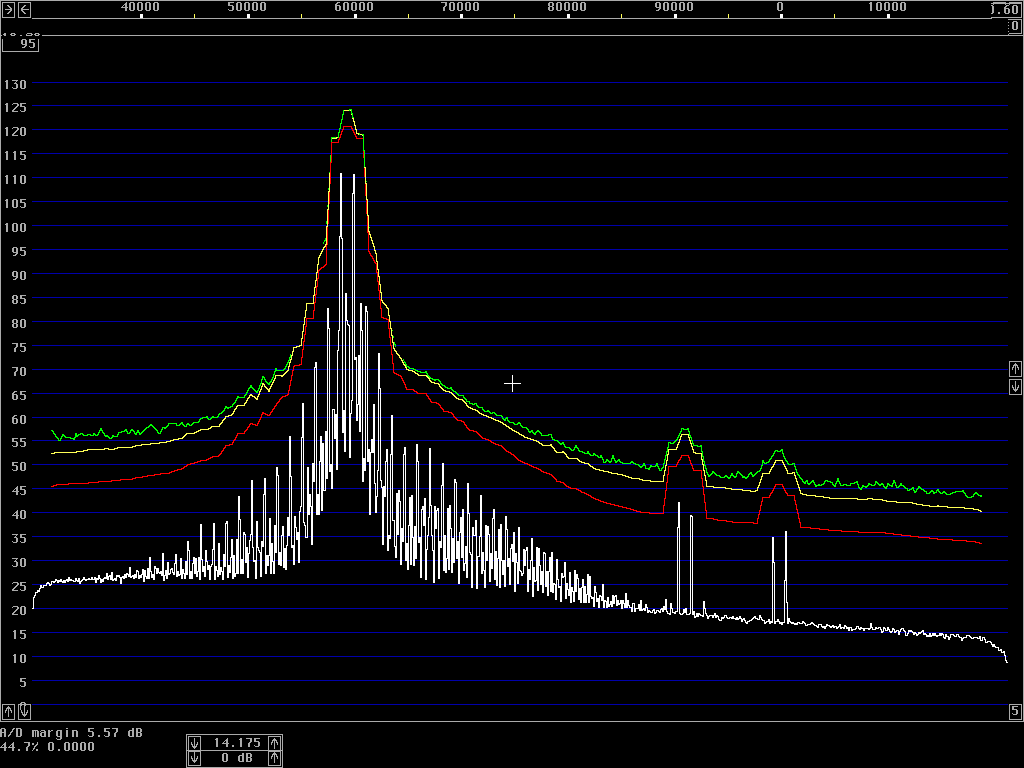
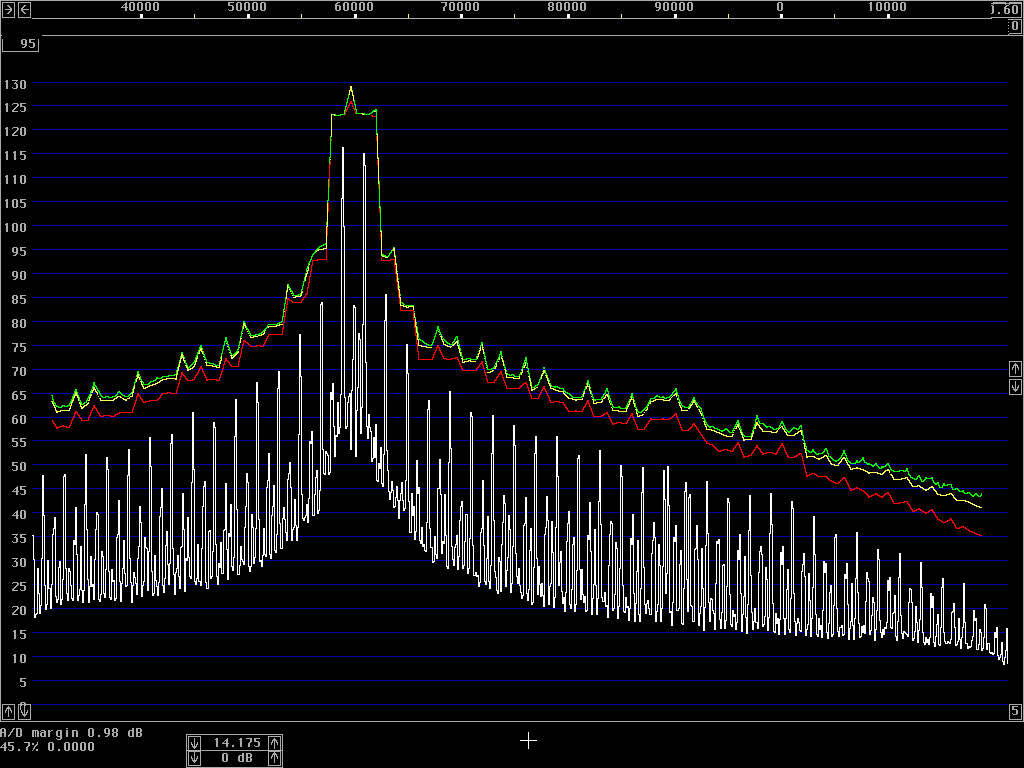
The average power spectrum is what we use to show the sideband noise of an unmodulated carrier. When a carrier is modulated, the total power emitted (averaged over the entire transmission) is typically lower by 3 dB in CW and by 10 dB in SSB. At large frequency separations, the average power spectrum will show correspondingly lower levels; but at close separations the average power spectrum may actually increase due to the tails of the modulation sidebands.

The correct procedure to measure the average power spectrum is to use a true RMS detector. The resulting power density in dB/Hz is then independent of the bandwidth, for all bandwidths that are narrow enough to have the same power density. A narrow filter is just averaging the power over time within its bandwidth – and when the detector is measuring true power it does not matter whether the averaging is done in narrow filters in front of the detector or in integrators after the detector. To get a smooth noise floor one normally has to average after the detector, over time; but one might equally well use very narrow filters and average over a range of frequencies. The results would be identical.

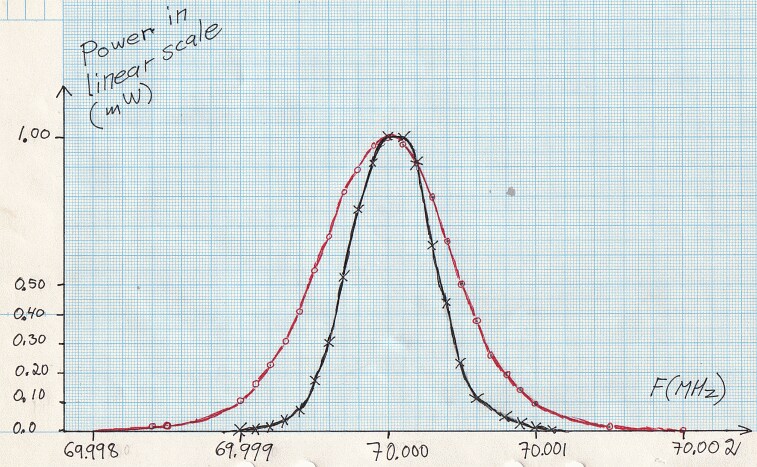
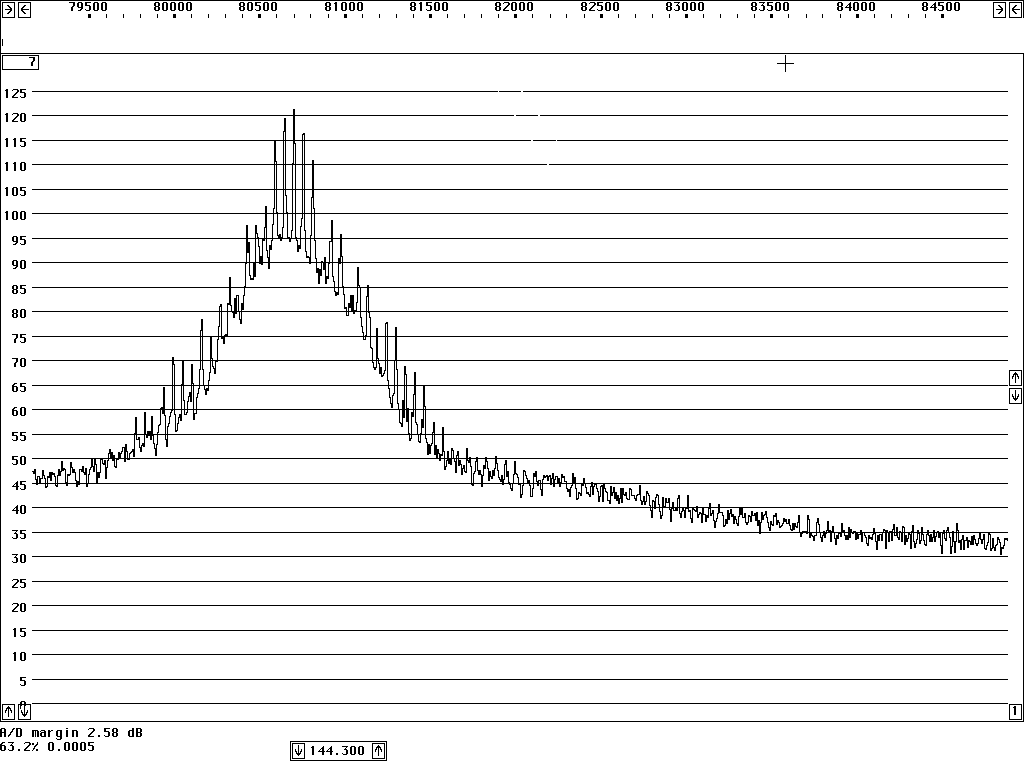
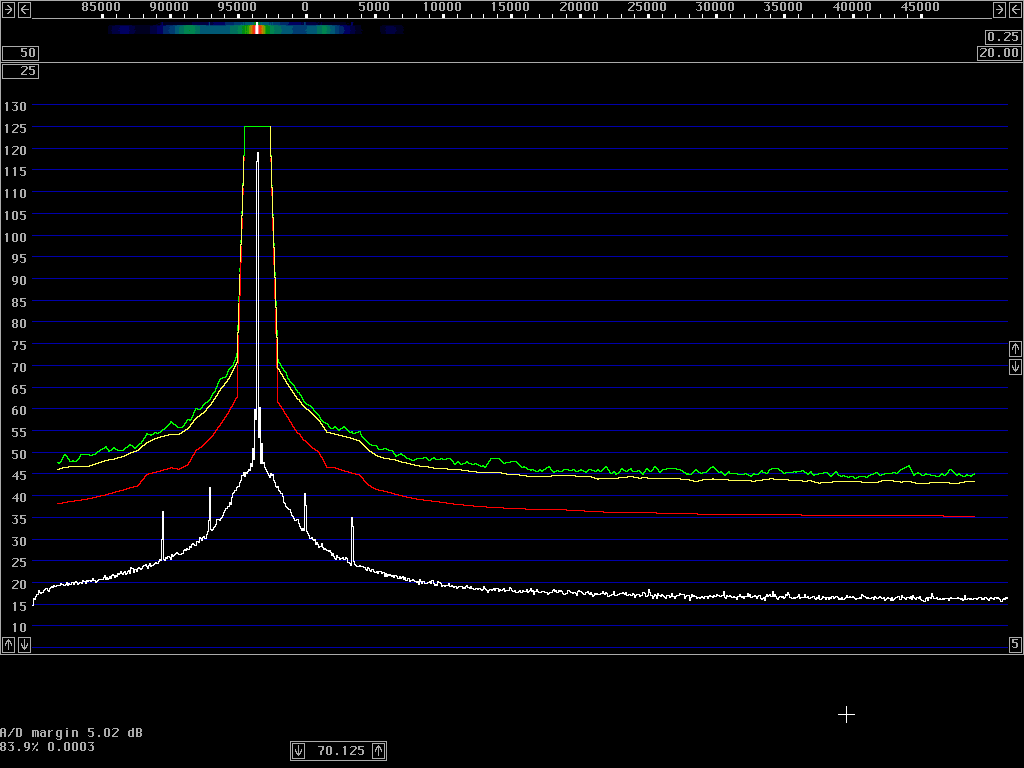
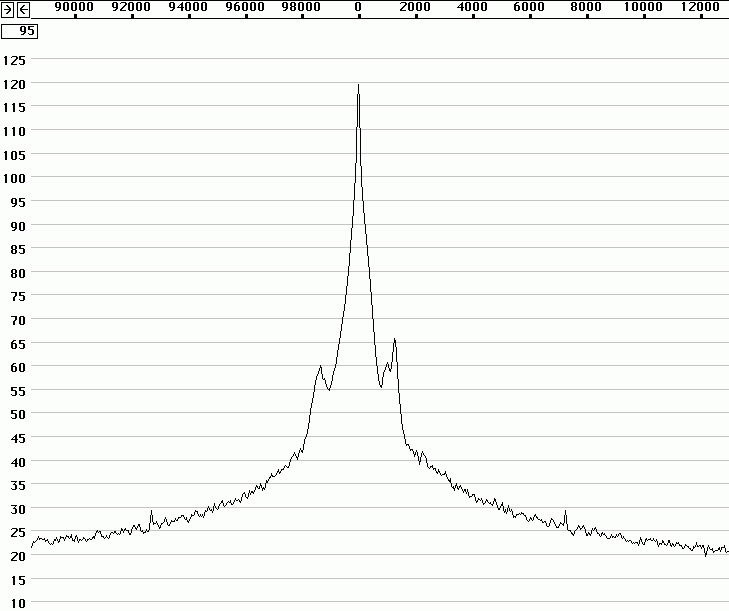
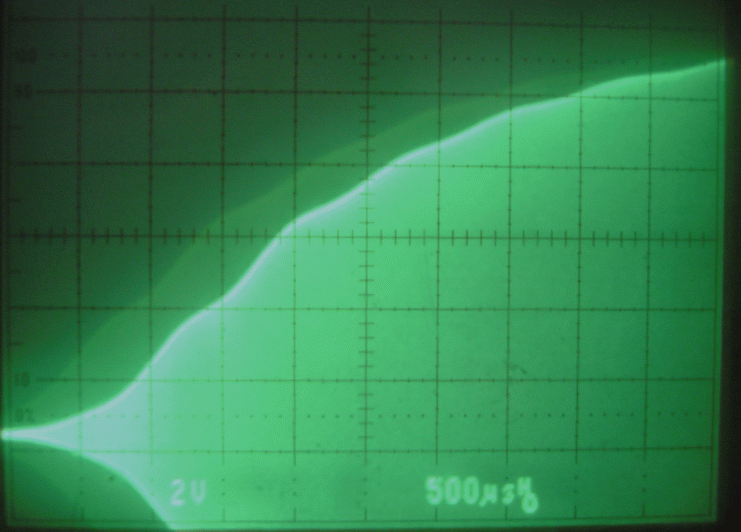
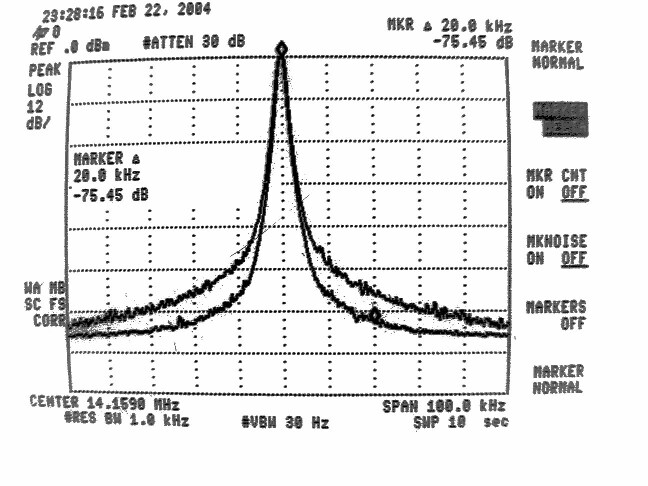
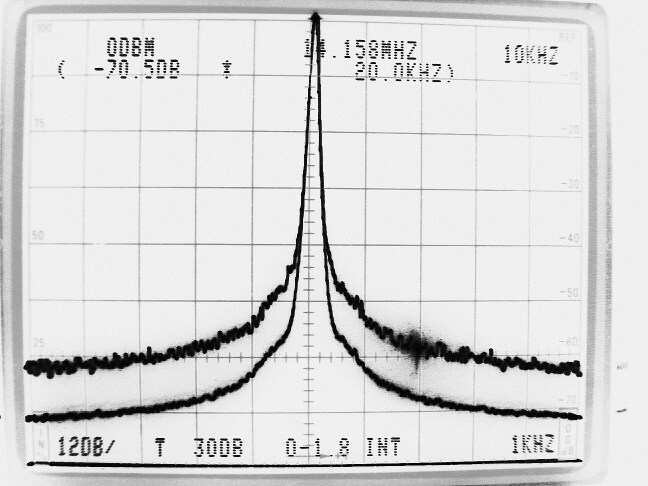
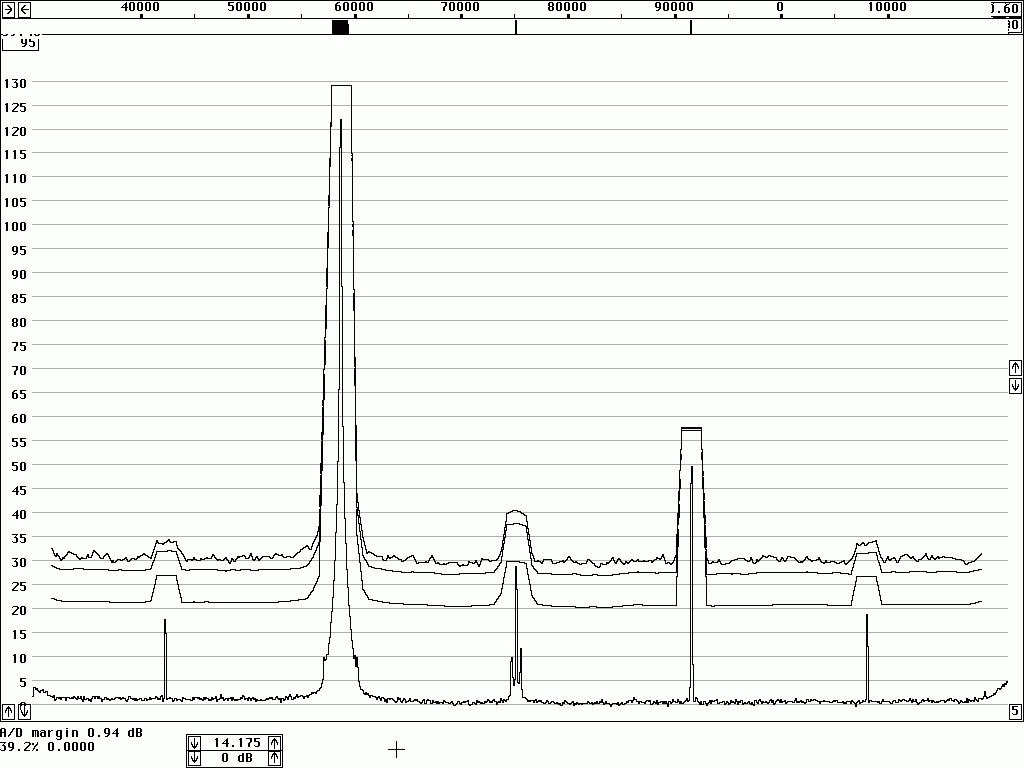
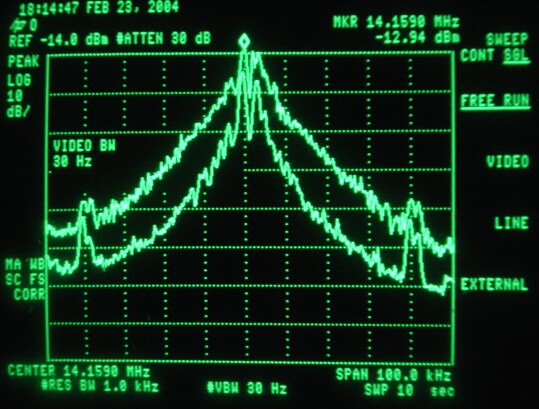
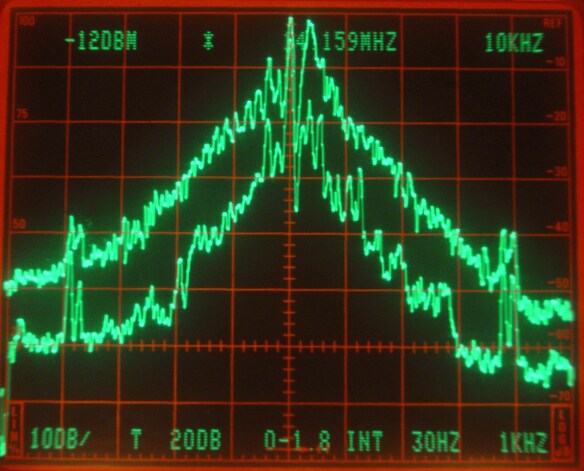
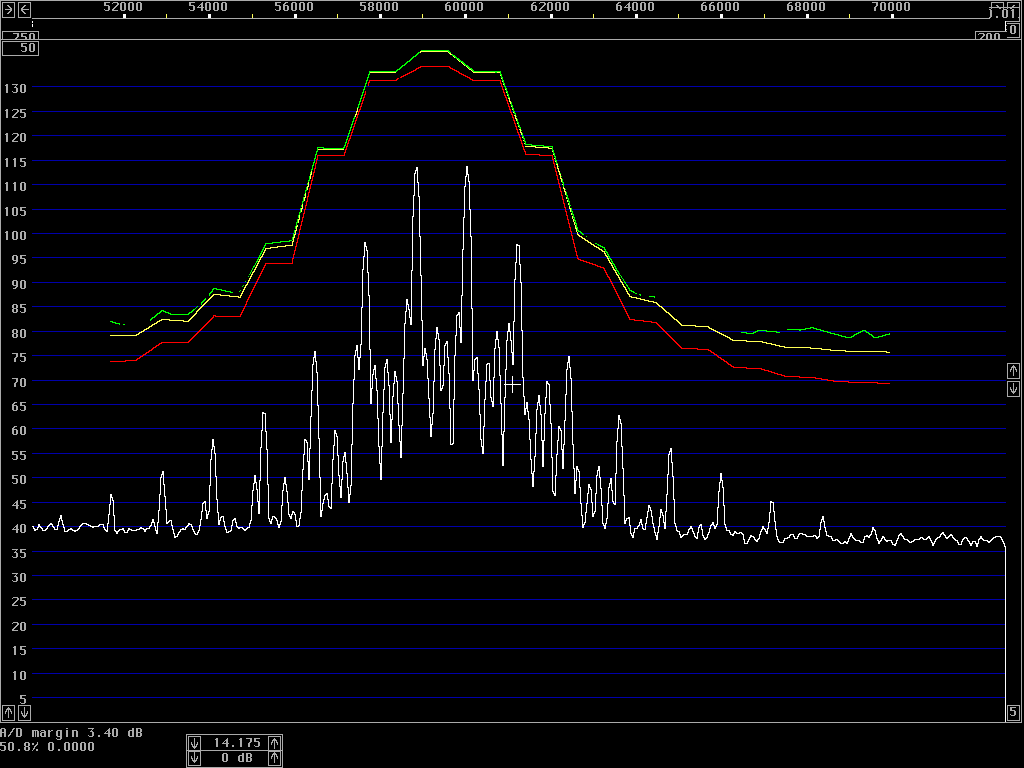
However, spectrum analysers typically have logarithmic detectors. It seems there are standard procedures that specify that the smoothed reading on a spectrum analyser has to be below some specified limit. The limit is then not truly in dBc/Hz but there is a bad habit among engineers to put dBc/Hz on such numbers anyway. I have been told that there has been some controversy in the telecom industry whether the limits one has to comply with refer to dBc/Hz as given by true RMS detectors, or whether the limits refer to the readings one can get directly from a specified spectrum analyser. It seems to me that this controversy has led to confusion about what the notation dBc/Hz truly means. To make it perfectly clear - it is a good idea to express the concept in words. The noise floor power density in dBc/Hz is the ratio of the noise power in 1 Hz bandwidth to the power of the carrier. The power of the carrier is easy, it does not matter what bandwidth or detector one uses, the spectrum analyser is calibrated to always show the same level for a pure carrier. The noise power is different - the only way to measure it correctly is to use an RMS detector. A log detector shows a value that is 2.51 dB too low if the signal looks like white noise within the passband. Another thing is that the selected bandwidth of the spectrum analyser may be different from the true noise bandwidth. To illustrate the accuracy of sideband noise measurements from standard instruments I have fed noise and a signal to two different spectrum analysers, a Tektronix 2753P and an HP8591A. The test signal was a carrier at 70 MHz, –80 dBm from an HP8657A signal generator which was amplified in a deliberately noisy wideband amplifier. The resulting signal had a carrier at –44 dBm with a flat noise floor at –85.0 dBc/Hz as measured by Linrad [3] which uses DSP to provide a true RMS detector after a nearly perfect rectangular filter. Both spectrum analysers gave noise floor power densities that did not depend on the bandwidth setting, within a few tenths of a dB. The value obtained from the 2753P was –88.8 dB/Hz while the result from the 8591A was –86.6 dB/Hz. These were the uncorrected values obtained directly from the carrier and noise floor levels and the nominal instrument bandwidths. For the 8591A, the bandwidth refers to the –3dB points of a filter that is close to Gaussian while the nominal bandwidth of the 2753P refers to the –6dB points of a filter that is relatively flat and has steep skirts. A spectrum analyser is an excellent instrument to measure its own frequency response, by simply sweeping across a carrier. Figure 1 shows the responses of the nominally 1 kHz filters in linear power scale. By numerical integration it is possible to find out what bandwidth a perfectly rectangular filter should have to give the same area under the curve as the one observed. (With 10 data points for each kHz, it amounts to taking the sum of all the data points and divide by 10 to get the noise bandwidth in kHz.) For the 2753P the noise bandwidth turned out to be 722 Hz while it was 1.14 kHz for the 8591A. The logarithm of these numbers give corrections in dB which add to the 2.51 dB correction for using a logarithmic detector. The theoretical correction for the 2753P was thus +3.94 dB while it was +1.94 dB for the 8591A. Applying these theoretical corrections one gets the noise floor of the above experiment as –84.9 dBc/Hz from the 2753P and –84.7 dBc/Hz from the 8591A; both corrected values were now in fair agreement with the value –85.0 dBc/Hz obtained from Linrad.

Measurements of amateur transmitters with sideband noise levels in the range –110 to –140 dBc/Hz at a frequency separation of 20 kHz can be done in many ways. Most popular is to use a good crystal oscillator and a high level mixer to shift the carrier frequency to near zero. The carrier can then easily be removed with a high pass filter [4]. The noise spectrum is then measured at audio frequency. One will get the noise from both sidebands so one has to correct by 3dB for that, as well as for the bandwidth and the detector if something other than a RMS detector is used. This method is used by ARRL lab in the composite-noise test for the QST product reviews, but some of the corrections are neglected [4] and the results published in QST are more optimistic than the results I find, by about 5 dB.

Another way is to use a good receiver and an attenuator. The receiver should be run in CW or SSB mode without AGC and the output level should be measured with a RMS voltmeter. This way one gets the signal and noise levels directly, one just has to know the frequency response of the receiver to calculate the noise bandwidth.


Figure 1: The 1 kHz filters of Tektronix 2753P and of HP8591A spectrum analysers. Numerical integration of these curves gave bandwidths of 722 Hz for 2753P and 1145 Hz for 8591A.

By using Linrad with appropriate hardware one can measure spectra directly. The Linrad S-meter uses a true RMS detector. With the WSE converters [5] the noise floor is at –145 dBc/Hz, which is good enough to measure any commercial transceiver on the market today.

It is also possible to use a standard spectrum analyser such as the 2753P or the 8591A together with a notch filter. When the transmitted signal is centred on the notch, the dynamic range requirement on the spectrum analyser becomes much smaller. By reducing the level of the main signal (the carrier for CW, or the wanted sideband for SSB) by about 50 dB, one improves the dynamic range of the spectrum analyser by a similar amount. This way of doing measurements has the advantage that one can monitor wide frequency ranges and locate spurs and instabilities that occasionally produce signals far from the desired frequency.

The averaged power spectrum is in itself a standardized measurement when given in dBc/Hz. The bandwidth has to be narrow enough to resolve narrowband spurs but there is no need to specify what bandwidth to use for this particular measurement.

Peak power measurements

For white noise, the peak-to-average power ratio depends on the time of observation. For reasonable observation times, the peak power is about 10 dB above the average power regardless of the bandwidth. A carrier or a narrowband spur has the same peak power as average power, but sidebands caused by modulation typically behave differently. In particular, keying clicks are wideband transients that behave like car ignition noise – they have a peak power that increases with the square of the bandwidth. (This is easy to understand, because filters smear a single short pulse out over time by an amount that is inversly proportional to the bandwidth. If the bandwidth is widened from 240 Hz to 2.4 kHz, the keying click will be 10 times shorter. This factor alone would make the pulse power 10 times higher if the total energy content of the pulse was unchanged. However, with 10 times more bandwidth, there is also 10 times more energy in the pulse so the power will increase with bandwidth by a factor of 100 in total.) Not only keying clicks behave like this, but also pulses such as those that may occur when the PTT button is pressed. SSB splatter is typically generated when the ALC voltage makes a jump because the drive level is going too high. The abrupt gain reduction causes a wideband modulation that is very similar to a keying click.

Peak power measurements need a standardised bandwidth. I find it natural to use SSB bandwidth, 2.4 kHz or what comes nearest in the available equipment. Well designed transmitters do not have tails in the modulation sidebands because they filter the baseband signal well enough, and also they do not have non-linearities that widen the modulation bandwidth by large factors. Just by using a relatively large bandwidth and by looking at the peak power using the max hold function of a spectrum analyser, one can see if a transmitter produces wideband transients even if it happens infrequently. The exact level of the transients is not so important – the really important thing is that they should not occur at all! Any observation that they do occur is an indication of a design error. Compared to that, whether they are observed in a bandwidth of 1 kHz (2753P), 2.4 kHz (Linrad) or 3 kHz (8651A) is really not very important. This illustrates the difference mentioned earlier between a production or type acceptance test, and a development or review test. The first needs strict protocols and calibrated equipment; the second does not – it only needs resourcefulness, to seek out bad performance caused by design errors, and an unwillingness to accept poor performance.

Keying waveforms and key clicks

To illustrate what this all means, I have made some measurements on keyed CW waveforms. Figure 2 shows the time domain waveform of a keyed signal at 14 MHz and Figure 3 shows the same signal as it looks on the 2753P screen at a resolution bandwidth of 100 Hz.

Figure 2: The time domain waveform of a keyed signal. The keying rate is 110 dots per second, corresponding to about 250 WPM. The waveform is in complex format with I and Q 90 degrees out of phase.


Figure 3: The spectrum of the signal shown in Figure 2 as seen on a Tektronix 2753P spectrum analyser. The scale is 10 dB/div and 2 kHz/div and the filter in use is 100 Hz.

Figures 2 and 3 are produced with a HP8657A signal generator by feeding the AM modulation input with a square wave through an RC filter. These waveforms are identical to the waveforms that have been presented as “the optimum keying waveform” in the ARRL Handbook for many years. This is incorrect, because simple RC shaping is inadequate - good transmitters use much better solutions [6]. The problem is that the keying clicks only decrease by 12 dB each time the frequency offset is doubled. It may not look so bad on Figure 3, but the limited dynamic range of a normal spectrum analyser does not really show what this signal sounds like on the bands... the keying sidebands extend on and on... the keying sidebands extend on and on... The 2753P spectrum shows the average power in 100 Hz bandwidth, but the peak power is higher – and it increases by 6 dB for a doubling of the bandwidth. Figure 4 shows the same signal as it looks on the zoomed in Linrad screen. The keying waveform has the same time for key up as for key down, the separation between the keying clicks is 4.5 ms and every second pulse is a key down while the ones in between are key up. The key up pulse and the key down pulse are equal in amplitude but they are opposite in phase.


Figure 4: The same signal as in Figure 2 as seen on the Linrad screen when zoomed in. The width of this spectrum is about 5 kHz. Here the individual keying sidebands are well visible. Note that the sidebands of even order are weaker. This is because the modulation before RC filtering was a square wave with 50% duty.

When the FFT spectrum is computed over a long period of time there will be many pulses within the computation time slot. As a result one will not see the spectrum of an individual pulse, one will see narrow spectral lines that are separated by the pulse repetition frequency. Every second spectral line is weak, because every second pulse is in antiphase. Another way of thinking about Figure 4 is that it shows the carrier and the modulation sidebands of an AM transmitter that is 100% modulated with a square wave that has first been filtered through a single RC time constant. The sidebands are symmetrical, so the keying clicks are equally bad at both sides. The sideband spectrum at each side of the carrier is of course the spectrum of the modulating signal, namely the keying waveform. A perfectly symmetric square keying waveform does not have any even harmonics, so as one would expect, the keying sidebands corresponding to even-numbered harmonics of the keying waveform are weaker than those of the odd-numbered harmonics. As expected, the amplitude of the side carriers decrease by 12 dB each time the frequency separation is doubled because that is the rate at which the overtones to a square wave rolls of in a simple RC filter.

When keying at 250 WPM, the 23 dB bandwidth is about 600 Hz according to the ARRL Handbook [7]. 100 times further out, at 60 kHz, one would consequently expect the level of the keying clicks to be 40 dB lower or at –63 dB relative to the desired signal. This is a terrible QRM level! High-speed CW stations should absolutely not use this primitive RC shaping for keying waveforms!

At lower speeds, the keying sidebands are more closely spaced and there are obviously fewer keying clicks in a given time. Also the sidebands will smear out, and dashes and word spacings will form components of lower frequencies that make the spectrum look very different in high resolution. When the bandwidth of the spectrum analyser is set wider, several of the keying sidebands will pass through the filter simultaneously. These signals have a particular phase relation and they add to form pulses – one for each make or break of the Morse code. In a wide bandwidth, the spectrum does not depend on what is being keyed. The average noise level created is simply proportional to the keying rate (the number of clicks per second) but the peak noise level is independent of the keying rate. Each key up or key down is a separate event that produces a wide-spectrum pulse that is unaffected by other keying events.

Figure 5 shows the Linrad screen in “TX test mode”. This is a mode I added to Linrad in order to have all the transmitter measurements done simultaneously. Here one can see the average spectrum and the peak hold spectrum at the same time. There is also an averaged peak spectrum with a time constant of about 1 second. Transmitters may emit short splatter bursts occasionally depending on the modulating voice. The peak hold will just go to the peak value the first time, and one will not see how often it happens unless the reset button is pressed each time. The averaged peak spectrum with a 1 second time constant shows these splatter bursts well, and it helps to find out how to speak into the microphone to make them really bad. One can then record the average and the peak hold spectra for evaluation in a worst-case situation.

As can be seen in Figure 5, the peak power of the keying clicks is 87 dB below the peak power at a frequency separation of 50 kHz while the average power is 98 dB below the peak power. The bandwidth is 2.4 kHz so the average interference power is -132 dBc/Hz. The reason for much better results than expected from [7] is that the keying for this test is far softer than one would use in real life at a dot rate of 110 Hz (132WPM, 660LPM).


Figure 5: The signal of Figure 2 as seen with Linrad in TX test mode. This image shows the spectrum up to 50 kHz above the carrier. The bottom trace is the average power spectrum in an FFT bandwidth of 12 Hz, the same as in Figure 4. The screen has only 1024 pixels so each pixel is the average of 24 FFT bins. This is the reason that the amplitude of the carrier is low. The upper curve is the peak hold spectrum in 2.4 kHz bandwidth. Very close to it is the average peak power spectrum. The curve in the middle is the average power spectrum in 2.4 kHz bandwidth.

This dot rate used in Figures 2 to 5 is quite realistic for CW meteor scatter, but such a high speed was chosen primarily to allow both the rising and the falling edge to be seen in detail in Figure 2 and to make the spectral lines well separated in Figures 3 and 4.

The ARRL Handbook claims that the simple RC filter used here would be appropriate for keying rates in the order of 30 WPM if it were implemented in an amateur transmitter. But the discussion of Figures 2 to 5 shows that keying a transmitter like this is not acceptable. Using a simple RC filter at high keying speeds will cause excessive and completely unnecessary bandwidth, and too much interference to fellow amateurs. At a modest keying speed, the time constants can be made 5 times longer and then the spectrum will be 5 times narrower so the keying clicks will produce an average power level of –132dBc/Hz at a frequency separation of 10 kHz. This is similar to normal sideband noise levels so it would not be a problem if the keying were perfect otherwise. There is still another problem, however: the output RF voltage has to follow the keying voltage strictly proportionally all the way from zero. Any non-linearity will increase the bandwidth. In a typical form of non-linearity, the output voltage to the antenna will be zero not only for zero keying voltage, it will stay zero for small values of keying voltage and only then start to grow linearly. The output is identical to the output that would be obtained from a perfect AM modulator that is fed from a non-linear amplifier with distortion at the onset of the waveform. This is similar to cross-over distortion in audio amplifiers, which creates harmonics of modest amplitudes but extending to a high order. In other words, this kind of non-linearity will increase the levels of the keying clicks, particularly at large frequency separations. A similar effect can be obtained by feeding a keyed signal through un-keyed class C amplifiers. Considering the levels of high order suppression for sidebands required in amateur radio, all of these effects are significant.

A good linear relationship between the voltage output from the keying filter and the RF voltage at the antenna is therefore very important. I have discussed the shortcomings of the simple RC filter in detail so that you can understand the basic problems. What you see in Figures 2 to 5 is real life data produced by actually keying an RF signal. The theory is of course well known and predicts exactly what one can see from the figures. A detailed theoretical treatment is presented in [8]. The very basic facts are: Each individual key-up and key-down transition generates a full-amplitude, full-spectrum click. The only thing that is "worse" about HSCW is that there are simply more clicks. The meaning of “full-spectrum” here is of course the full frequency response of the keying filter, mirrored around the carrier, and broadened by any distortion due to the non-linearities between the keying waveform and the RF output voltage waveshape. The problem with using very high speed CW for meteor scatter is that one has to modify the keying circuits for much shorter time constants in order to have any keying at all, thereby making the rig awful at all keying speeds. To avoid this it may be much better to key an audio tone and feed it into the SSB microphone input. The SSB filter will then limit the bandwidth to 1.8 kHz. By setting the drive level properly so that ALC circuits do not distort the waveforms, one can produce excellent HSCW.

It is not necessary to look at both the time domain and the frequency domain to decide if the keying is OK or not. One can look at either the time domain in Figure 2 or the frequency domain in Figure 4. Both of them contain all the information – because both are generated from the same RF signal and one is the Fourier transform of the other. (A few details here... Actually the time function is the backwards transform of the frequency spectrum but forward and backwards transforms differ only in the phase. Otherwise it is the same algorithm. Also Figure 4 is not really the Fourier transform, it is the power spectrum of the transform, but the relevant information is still there.) A signal that is wide in the frequency domain is narrow in the time domain and vice versa. The width in the time domain is the width of the envelope, the sinewave under the envelope gives the frequency of the signal which gives the peak position in the frequency domain. The Fourier transform is a linear transformation which means that a signal can be split in several parts that sum up to the signal itself. The sum of the Fourier transforms of all the parts will then sum up to the transform of the total signal. A single Morse code transition like the rising edge in Figure 2 has a spectrum that looks like a line that joins all the peaks of the spectral lines in Figure 4 but with smaller amplitude. When the Fourier transforms of many such individual transitions are summed, the phase of all of them will be equal at frequencies corresponding to frequency offsets that are multiples of the repetition rate. At frequencies in between the contributions from the different pulses cancel because they have opposite phases. As explained in [8] the width of the time function is the width of the transition from on to off or off to on. The length of the key down and key up periods will only affect the repetition rate and the spacing of the sidebands in the frequency domain.

An exponential RC-generated rise time such as in Figure 2 gives a spectrum that rolls of by 12 dB per octave. However, the optimum shape of the pulse for a Morse code dot is a Gaussian. The Gaussian shape is special, because it is the mathematical function that minimizes the width simultaneously in both the time domain and in the frequency domain – the Fourier transform of a Gaussian is another Gaussian. (This is why the HP8591A uses Gaussian filters – they allow the fastest possible sweep without loss of amplitude accuracy. The TEK2753P with its more rectangular filters has to sweep more slowly, but it allows much better viewing of weak signals close to a strong one.) For a single transition, key down or key up, the optimum shape is a Gaussian ‘error function’. This is an S-shaped function that avoids the sudden transitions and will produce a Gaussian spectrum shape with the fastest possible roll-off, 10dB per 30Hz increase in the frequency separation at typical amateur keying speeds. (For details see [8], equation 20 and Figure 5.)

Modern rigs typically generate CW by keying a signal which is then passed through the SSB filter and therefore the keying clicks should not reach outside the bandwidth of the SSB filter. This is one way of producing nearly ideal rise and fall waveforms. One example is the IC706MKIIG, which generates the waveform of Figure 6 on 144 MHz when keyed at 55 Hz. A comparison with Figure 2 immediately shows that this keying is much better. The envelope looks like the output of a higher order filter, and it does not have the steep onset of a square wave filtered through a RC filter.

Figure 6: The keying waveform of IC706MKIIG at 144 MHz. The keying is 55 Hz square wave.

The spectrum of the keyed IC706MKIIG corresponding to Figure 6 is shown in Figure 7. In a comparison between the keyed spectrum and the continuous carrier of this station, one can find that the interference level from the keyed rig is below the interference of the un-keyed carrier at frequency separations above 700Hz.

That is the point where the keying clicks disappear into the sideband noise of the un-keyed carrier. Note that the keying sidebands fall off at a rate of about 12 dB for every 200 Hz while the simple RC filter gives sidebands that fall off by about 12 dB for a doubling of the frequency separation. At large frequency separations this makes a big difference, and the keying spectrum of Figure 8 is much narrower than the spectrum of Figure 4, by much more than the factor of 2 that would be produced by the simple difference in time constants.


Figure 7: The spectrum of the signal shown in Figure 6, an IC706MKIIG keyed at 55 Hz on 144 MHz.

It is quite clear that excellent keying is possible: very low keying clicks in combination with a waveshape that sounds sharp and clear, and also has the potential to go to high keying speeds. The simple RC filter belongs to the era of cathode-keyed vacuum tubes; there is no reason to use such a primitive filter in modern equipment... no reason, that is, except for poor design.

Effects of ALC

The discussion about CW waveforms up to this point was intended to show principles of normal keying. In the real world there are additional complications. Figures 8 and 9 show the time domain waveform and the spectrum of the same IC706MKIIG when it is keyed on 14 MHz. One can clearly see something happen that reduces the output power, after it has risen above the steady-state value it will have during most of the key down time. Most probably this is the ALC setting the power at the desired level, but with some overshoot.

The spectrum shown in Figure 9 is the Linrad TX test mode display corresponding to Figure 8. The keying rate is lower compared to Figure 5 so there are fewer keying clicks each second. Therefore the peak levels are 25 dB above the average power levels in 2.4 kHz bandwidth. The peak hold and the 1 second peak average curves are close to each other, differing by about 3 dB only. This is because the peak level is determined within the time spanned by one FFT (actually the time between the – 6dB points in the FFT1 window function) and there is one new maximum value about every second. On the air, the keying clicks at these levels make a 10 kHz segment of the 14 MHz band useless. The peak power of each key-down click is only 34 dB below the full power of the carrier at a frequency separation of 5 kHz. I think the reason for this bad behaviour is the mis-use of the ALC that seems to be a common plague in amateur transceivers. Figure 8 points in this direction, as well as the fact that the amount of overshoot depends on the time since the previous key-down period. If it is short enough, the ALC voltage does not have time enough to change much and therefore the gain adjustment becomes very small each time a new pulse arrives.


Figure 8: Keyed waveform of IC706MKIIG at 14 MHz. The reason for this waveform is probably the ALC. It is bad practice – but very common – to use a fast ALC to set the drive power at the desired level. The fast feedback required to bring the gain down rapidly causes wideband modulation that takes the form of keying clicks in CW and splatter in SSB.

The keyed waveform of the IC706MKIIG in full breakin mode is much worse than that shown in Figures 8 and 9. The spectrum is shown in Figure 10. This level of keying clicks is not acceptable at all. Not only is the close-range interference level worse than in normal (semi-breakin) mode, there is also a wideband component with a flat spectrum that has peak power levels 75 dB below the carrier in 2.4 kHz bandwidth. An inspection of the time domain signal shown in Figure 11 indicates that the main problem in full breakin is that the ALC voltage is being reset during every single key up, causing the ALC voltage to need a very large change to get the right output power. Keying then produces a damped oscillation at about 5 kHz in the ALC loop, which in turn produces amplitude modulation at a peak level of about 15% as one can see in Figure 11 by close inspection. The resulting 5 kHz sidebands have a peak amplitude that is only 23 dB below the carrier as can be seen in Figure 10. It is a general rule (of course) that major deficiencies in a transmitter are well visible in both the time domain and in the frequency domain. The similarity of Figures 9 and 10 indicates that the keying clicks are created by the same phenomenon.


Figure 9: The spectrum of a IC706MKIIG on 14 MHz. The keying speed is 55 Hz and the duty cycle about 25%. The keying clicks disappear if the key-up time is made very short. The mode is BK with a long delay time to ensure QSK is inactive.


Figure 10: The spectrum of IC706MKIIG when hand keyed at 14 MHz in full breakin mode.


Figure 11: The time domain function of the IC706 when keyed in full breakin mode. In this mode the ALC loop has to make a large gain adjustment at every key down, as compared to the semi-breakin mode of Figure 8, and therefore the amplitude gets modulated by an oscillatory behaviour in the ALC loop, corresponding to nearly 15 % AM modulation at a frequency of about 5 kHz. This is the cause of the sidebands visible in Figure 10. f

The wideband interference visible in the spectrum in full breakin mode is even more easily understood by inspection of Figure 12, which shows the time domain function at the start of every dot or dash, magnified by 40 dB relative to Figure 11. At the moment when the antenna relay contacts switches the antenna to the TX, the dot/dash has already started and the power is already at about –70dB relative to full power. The cure to this problem is easy. The keying is obviously done in at least two stages and they do not have their zero points at the same point on the keying waveform. Just changing the zero point of the keying voltage, that is causing the power to be turned on too early, will remove this keying click without any adverse effect at all.

Figure 12: The onset of the keying waveform in full breakin mode for the IC706MKIIG at 14 MHz. The magnification is 40 dB relative to Figure 11.

Figures 11 and 12 make a good illustration to the principle of additivity in Fourier transforms. The waveform can be written as the sum of three waveforms. The dominating part is the waveform displayed in Figure 6. To this is added a pulse with about 15% amplitude which is a damped oscillation with several peaks at a modulation frequency of about 5 kHz. The spectrum of the main part is of course identical to the spectrum of Figure 6. The shape is obtained by joining the peaks of the individual spectral lines in Figure 6 while the amplitude of the sidebands is lower by the rate of pulse repetition rates. The pulse structure provides the sidebands at 5 kHz, but the pulses are not quite sinewave in shape so they contain components of overtones which are sidebandsfurther away from the carrier. The third component can be seen in Figure 12 only. It is a small pulse with very short risetime. The risetime is probably much shorter than one can see in Figure 12 because the display is limited by the bandwidth of the Linrad system. This pulse gives a click that has the same amplitude over the entire spectral range, and it is this component of the total waveform that is responsible for the wideband clicks.

When looking at a waveform in the time domain, the bad part is any place where the second derivative of the envelope is large – in other words, any place where there is a sharp corner. Such places occur at the onset of both key up and key down in the simple RC-shaped keying shown in Figure 2; but there are no such points in the much better waveshape of Figure 6. Large second derivatives may also occur when an amplifier saturates or when the transmitter gain is changed abruptly because of ALC action. Badly designed QSK is another source of large second derivatives as we see in Figure 12.

Figure 13 is a reference spectrum at 14 MHz for the unmodulated IC706MKIIG used in this article. It is neither especially good or bad, –122 dBc/Hz at 20 kHz, but the difference in the spectra when the carrier is keyed is horrible. On 144 MHz on the other hand, there is no visible difference between the keyed and the unkeyed spectrum at frequency separations above about 700 Hz as was pointed out in the discussion about Figure 8.


Figure 13: The IC706MKIIG without keying on 14 MHz, for comparison with Figures 9 and 10.

Another transceiver that has a poor reputation for key clicks is the FT-1000 range. As often happens with such problems, opinions range from “All [models of] FT-1000 as shipped from the factory click excessively and needlessly, ” to the complete opposite – denial that any such problem exists. As seen with the eyes of a VHF weak signal enthusiast, the FT1000 is not so bad, but on crowded HF bands the keying clicks present a real problem to fellow amateurs.

It is (like always) not difficult to adjust components for reasonable rise and fall times. Modifications, sound-clips and composite spectra of these transceivers before and after modifications can be found on the Internet [9]-[11]. It seems like normal variations in component parameters and perhaps other differences cause some difference in rise and fall times for the FT1000 range of transceivers. The unmodified FT1000D that I have used in this article has a somewhat softer keying compared to [9].

The peak hold spectrum in 2.4 kHz bandwidth is excellent, but the high-resolution average power spectrum reveals clicking sidebands at +/- 1.2 kHz from the carrier as can be seen in Figure 14.


Figure 14: Expanded average power spectrum of a keyed FT1000D on 14 MHz. The keying is 50% duty with 25 dots/sec. The FFT bandwidth is 50Hz.

The sidebands are caused by AM modulation on the rising edge, something that is well visible on the oscilloscope as can be seen in Figure 15.


Figure 15: Rising edge of keying waveform of a FT1000D on 14 MHz.

As can be seen from Figure 15, the AM modulation starts at an amplitude corresponding to about 5 % of the full carrier amplitude. This means that the modulation sidebands at Ý 1.2 kHz appear at about 30 dB below key down power. The AM modulation lasts about 2 ms, which is 5% (–13 dB) of the keying period time. One would therefore expect the keying click sidebands at –43 dB in a 500 Hz wide filter. In the frequency domain, Figure 14, the level is about –60 dB in 50 Hz bandwidth in fair agreement with this rough estimate. At frequency separations above 1.8 kHz there are no key clicks at all, only the carrier sideband noise, which is 50% below its normal level due to the keying at 50% duty.

The 1.2 kHz keying click sidebands of the FT1000D are not at all affected by the ALC. These sidebands are produced by AM modulation in the keying circuitry and the spectrum does not change when the output power is reduced

ALC and SSB

ALC is just a DC-coupled AM modulator which will add the spectrum of the ALC signal to both sides of the carrier. But if the ALC signal has a fast rise, slow decay characteristic, the bandwidth of the added modulation becomes very large. It is then essential that the modulation amplitude is very low, otherwise the interference generated becomes a problem. Unfortunately this is a problem in many transceivers – in fact it is a problem in most of the transceivers I have looked at. For a detailed discussion, have a look at [12].

Using ALC to provide voice compression on SSB is a bad habit from old times. It was not a good idea back then and it is really stupid in modern equipment. The ALC causes a lot of terrible splatter for no good reason at all. I have been told that amateurs want to watch the ALC meter to be sure the rig operates at full power. It would be much better to remove the control function and instead detect the drive level and show that on the meter. Driving the power amplifier slightly into saturation is not quite as bad as adding wideband modulation through the ALC. There could be some safety circuitry to protect the amplifier if necessary; this could work like the current ALC systems do, but it should be set for a somewhat higher level that should never be reached in normal operation. Modern transceivers with computer control could easily set the drive level right for each band and mode without adding wideband modulation... if amateurs wanted it like that.

The linearity of the power amplifiers is typically good enough. The results obtained in two-tone tests do not correlate at all with the splatter generated. The intermodulation products are typically far below the ALC sidebands with real voice signals. In a two-tone test, the peak power is reached with a repetition rate of about 1 kHz, causing the saw-tooth waveform of the ALC to have a frequency of 1 kHz with very low amplitude. Therefore the two-tone test essentially shows the power amplifier linearity. But testing with a real voice into the microphone shows what signals other band users really will have to cope with – and that is often something quite different and much worse.

I have used the IC706MKIIG as an example on how the spectra in Linrad test screen relate to the time domain waveforms. Changing from Morse code to SSB does not make any fundamental difference, except that it becomes much harder to look at the time domain waveform. The IC706 produces splatter on 14 MHz that seems to have the same origin in the ALC loop as the keying clicks (see later discussion about Figure 23). Another example is the FT817, which is shown in Figure 16. This particular unit must be regarded as faulty. I would not be surprised if the error is incorrect adjustment in the ALC circuit but I did not have the time to look closely.


Figure 16: The spectrum of a FT817 in SSB mode on 144 MHz. The splatter is due to an instability of some kind. The signal is clean at voice high levels, like when saying “Aaaaa” into the microphone, and also at low levels. Somewhere in between the splatter is terrible as this image shows. This unit must be regarded as faulty. I do not know how often this kind of error is present in these rigs but I have seen another one not having this error.

I do not think it would be difficult at all to eliminate the problems with the IC706MKIIG and the specific FT817 illustrated above. It probably amounts to reducing the gain a little to make the ALC less active. That is in theory. In real life it may be hard to do anything with miniaturized boxes like these transceivers. I have never looked inside so I do not know.

The peak power spectra in SSB bandwidth show the quality of transmitters in a way that is honest to the customer who tries to find out which transceiver to buy.

The measurement is extremely easy with an FFT-based analyser such as Linrad and the WSE converters as explained above. Just connect the transmitter to the WSE converter input through an attenuator and operate as normal. Linrad will catch the spectrum.

Like for the average power spectra it is of course also possible to use a standard spectrum analyser such as the 2753P or the 8591A together with a notch filter.

Measurements using notch filters

The standard instruments from Hewlett Packard and Tektronix, the HP8591A and the TEK2753P, have different filter shapes as discussed above. Hewlett Packard uses Gaussian filters which give faster response while Tektronix uses more rectangular filters which allow better visibility for sideband noise. Figures 17 and 18 show what the screens look like at a resolution of 1 kHz when these instruments are fed with the signal from a low noise crystal oscillator. The Linrad screen in “TX test mode” with a bandwidth of 2.4 kHz is shown in Figure 19.


Figure 17: Performance of the HP8591A spectrum analyser. The upper curve is peak hold and the lower curve is the average power spectrum. At 20 kHz the average spectrum is 75.45 dB below the carrier which translates to-101dBc/Hz. The peak hold spectrum is at about -65 dB with respect to the carrier. Note that the vertical scale is 12 dB per division.


Figure 18: Performance of the TEK2753P spectrum analyser. The upper curve is peak hold and the lower curve is the average power spectrum. At 20 kHz the peak hold spectrum is 70.5 dB below the carrier. The average power spectrum is 12 dB lower which translates to-111dBc/Hz. Note that the vertical scale is 12 dB per division.

The crystal oscillator used for Figures 17 to 19 has a sideband noise of about -169 dBc/Hz so these figures give the limitations of the instruments directly. Amateur transceivers produce sideband noise at about –125 dBc/Hz when emitting an unmodulated carrier. It is obvious that neither the 8591A nor the 2753P can be used to check their performance directly. Many transceivers emit splatter that is easily seen on the screen of these standard instruments, however. That is not because the instruments are especially good – the reason is that so many amateur transmitters are so bad.


Figure 19: Performance of the WSE converters with Linrad in TX test mode. Counting from top, the first curve is peak hold, the second is peak power averaged with the equivalent of a 1 second RC time constant, and the third and the fourth are average power spectra. The first three spectra are at a bandwidth of 2.4 kHz. At 20 kHz the average spectrum is 109 dB below the carrier which translates to-143 dBc/Hz. Because the system uses direct conversion, the spur at 91 kHz is the mirror image. The spur at 75 kHz is the DC offset and 1/f noise of the Delta44 surrounded by the low frequency magnetic field from a fan picked up by the Delta44. The spurs at 43 and 107 kHz are due to second harmonics inside the Delta44.

Comparisons between transceivers on SSB

The FT1000D allows proper operation in SSB mode. When operating according to the manual, the speech processor is used to set compression to 10 dB and the ALC circuit adds another 3 to 5 dB of compression, with some wideband splatter as a consequence. However, one can set the drive level to a point just below where the ALC starts acting, and then the speech processor can be used to set the desired compression, about 15 dB. For details, see [12] where you can find SSB spectra of the FT1000 that are representative of normal usage. Unfortunately the transmitter amplifier is noisy, when the gain is not turned down by the action of the ALC, the sideband noise produced by inadequate noise figure in the transmit amplifier is at –116 dBc/Hz for a steady carrier at a frequency separation of 20 kHz. When operating according to the manual, the sideband noise is at –120 dBc/Hz because of the reduced gain due to the ALC. The obvious solution would be to make a modification that provides a constant voltage that gives a permanent gain reduction.

The FT1000D typically produces a very clean spectrum when one speaks into the microphone like one would do in a QSO, but there are occasional outbreaks of splatter. Such splatter peaks seldom occur – it happens when I say a sound right between “Y” (as in YES) and the German “_” (as in _BER) into the microphone. This particular sound happens to generate essentially two sine waves that are separated by nearly 2 kHz. As a consequence the ALC does not generate any distortion to the waveform because the maximum power repeats at a rate of 2 kHz. This particular interference is generated by the cross-over distortion in the power amplifier and/or driver stages as will be shown below. The purpose of transmitter testing is to find the weak spots of each transmitter and to characterize them, so that users can minimize the problems and manufacturers will be able to improve the equipment. The weakest spot (worst case interference) of the FT1000D is that rare “Y/_” sound, which is a selective phenomenon and not a big problem in actual usage. For representative spectra in normal voice see [12]. The worst case interference of the FT1000D is shown in Figure 20. Figures 21 and 22 show the same as seen with the standard instruments from HP and Tektronix with a notch filter that removes the desired SSB signal.


Figure 20: Worst case spectrum on 14 MHz of an FT1000D in SSB mode, generated by the “Y/_” sound. Linrad in TX test mode.


Figure 21: Similar signal to Figure 20 but here as it looks on the HP8591A. A notch filter is used to remove the main signal and the upper scale line is 35 dB below the peak level of the SSB signal.


Figure 22: Similar signal to Figure 20 but here as it looks on the TEK2753P. A notch filter is used to remove the main signal and the upper scale line is 35 dB below the peak level of the SSB signal.

Figures 20 to 22 show the same thing. All three show the peak hold spectra and the average power spectra. In SSB mode the important information comes from the peak hold spectra, because the average power spectra are difficult to obtain in SSB mode on a sweeping analyser. It is not so easy to keep producing the worst splatter level by voice for the long time of a single sweep at a video bandwidth of 30 Hz, but the peak hold measurement is straightforward and easy in SSB mode on all three instruments and the average power spectrum is trivial to produce for a continuous carrier.

At a frequency separation of 20 kHz, the peak splatter level is –60 dB relative to the peak power in the Linrad 2.4 kHz measurement. The 8591A gives –63 dB in a bandwidth of 1.14 kHz while the 2753P gives –66dB in a bandwidth of 722 Hz. The splatter is neither pulses nor white noise so it is unclear how the peak amplitude relates to the bandwidth. The results indicate that the character of the splatter in this case is like white noise with a level of –60 dB in 2.4 kHz bandwidth.

The worst case speech waveform is different between different transmitters. Figure 23 shows the worst case emissions from an IC706MKIIG. This rig suffers from the ALC problems that were discussed above in conjunction with Figures 8 to 11 as judged from the similarity of the spectra. This particular rig does not produce much interference with the “Y/_ sound; instead, the worst case interference is produced by the sequence “A-A-A-A-A”, with the short “A” sound repeated at a rate of something like 5 Hz with less than 50% duty. The spectrum is displayed in Figure 23. Note that the peak power in the neighbouring channels is not even 20 dB below the power of the main signal, most probably due to the ALC malfunctioning. The IC706MKIIG splatter drops rapidly with increasing frequency separation and it is obvious that the mechanism is different compared to Figure 20.


Figure 23: Worst case 14 MHz spectrum of an IC706MKIIG in SSB mode.

Figure 24 shows the IC706MKIIG with the “Y/_” sound into the microphone. As expected, the splatter that is probably generated by the ALC is absent, the spectrum looks very clean and the cross-over distortion causing the problems in the FT1000D is obviously insignificant in the IC706MKIIG. Figure 25 shows the FT1000D with the “A-A-A-A” sequence into the microphone. The rig is operated according to the operating manual with full ALC. As shown in [12] the spectrum is even narrower without the ALC.

Figures 24 and 25 show very clearly that the waveform that one transceiver can not handle well is no problem at all for the other transceiver. It seems like almost every transmitter has its own peculiarities. Figure 26 shows the spectrum of a TS-520. For this rig there is not a single sound that could be found to make the worst interference, although the spectrum shape varies with the different sounds. Figure 26 shows the word “Echo” repeated rapidly. Saying several other words as well will lift the peak hold spectrum a bit higher, but not very much. The interference in the TS-520 is caused by the ALC, which was peaking about 25% of the ALC range according to the meter. By slightly mistuning the PA drive so that the ALC meter does not move at all, and setting the mic gain higher to give the same average output power, the splatter generated by the ALC can be removed. Operated this way the TS-520 emits a very clean signal. The difficult test cases, the “Y/_” sound and the “A-A-A-A” sequence are shown in Figures 27 and 28. Saying the word “Echo” into the microphone does not cause more splatter than the “A-A-A-A” sequence when the ALC is disabled.


Figure 24: 14 MHz spectrum of an IC706MKIIG in SSB mode with the “Y/_” sound into the microphone.


Figure 25: 14 MHz spectrum of an FT1000D with the “A-A-A-A” sequence into the microphone.


Figure 26: 14 MHz spectrum of a TS-520 with the word “Echo” repeatedly into the microphone. The unit is operated with ALC at about 25% of the ALC range.


Figure 27: 14 MHz spectrum of a TS-520 with the “Y/_” sound into the microphone. The unit is operated without ALC but with full output power.


Figure 28: 14 MHz spectrum of a TS-520 with the “A-A-A-A” sequence into the microphone. The unit is operated without ALC but with full output power.

Conclusions and discussion

Testing transmitters is a far more complicated task than testing receivers. It is complicated in the sense that it is very difficult to set up a standardised test that has a chance to be generally accepted, and that would be relevant as a figure of merit for the spectral purity of a modulated transmitter.

From a practical point of view it is very simple, however. Just modulate the transmitter in every possible way that is in accordance with the instruction manual. Collect the peak hold spectrum in an SSB bandwidth and present the graph with some notes on which kind of modulation the rig has difficulties with (if any). Not only spectra at full power should be investigated. Some rigs send out massive wideband pulses when the PTT is pressed or released, while others emit high levels of wideband noise during silent periods in SSB when the ALC does not reduce the transmitter gain. With a wideband FFT spectrum analyser it is easy to find the peculiarities of a transmitter and to measure the worst spectrum.

The measurement can also be made with standard instruments, if a notch filter is added to extend the dynamic range. It just takes some more time, because with a sweeping analyser a single transient will affect only one frequency at any given moment.

A modern transceiver should provide a peak hold spectrum like the old TS-520 in Figures 27 and 28, or better. But this is very far from what the measurements actually show – because transmitter quality is not receiving its due share of attention. Once this problem does begin to receive some thoughtful attention, it will be very easy to make improvements. Aside from silly things like emitting a very short pulse at full power when the PTT is pressed, most problems can be eliminated by reconfiguring the ALC, and by making sure there is an amplitude clipper at the right side of the SSB filter – the input side. There is also a need for some care to avoid excessive noise figures in the first transmit amplifier after the SSB filter, to prevent high levels of wideband noise (as in the FT1000D for example see Figure 25).

Two peak hold spectra, one in CW mode and another in SSB mode, will provide all relevant information about transmitter spectral purity that is needed for a product review.

The test engineer might want to show some more spectra, probably different for each transmitter, because there may be specific events like pressing the PTT button that make the spectra absolutely horrible. It then makes sense to show the spectrum as it looks when such events have been excluded from the time-frame of the measurement. Likewise it may be relevant to show spectra with VOX or QSK off, in case they differ significantly from the spectra when they are enabled. Such differences are of course due to design inadequacies that would be easy to correct, so the place where these measurements should be made first is in the manufacturer’s design laboratory!

There is an element of arbitrariness in the peak power spectra. Finding the special sound to make the FT1000D emit the horrible spectrum of Figures 20 to 22 was not so easy. The first test, saying “Aaaaa, testing, testing, one, two, three” a few times did not show anything unusual. If I had been satisfied with that, the outcome had been a result like the one in Figure 25. However, by trying various other phrases as well as speaking at several different voice pitches, it was not difficult to find a much worse peak hold spectrum. Once I knew there was something to look for, it was then fairly easy to find the exact sound to produce worst-case interference.

The FT1000D used in this article has a normal two-tone test result as one can see in Figure 29. It is a delicate balance, however, and by making the two tones slightly different in amplitude one can get much worse high order intermodulation. By increasing the separation between the tones one can also get a slightly worse result. Such a modified two-tone test is displayed in Figure 30. Note that it is very similar to Figure 20. The high order intermodulation that the FT1000D suffers from does not change when the output power is reduced, unlike the low order components. The high order intermodulation is caused by insufficient bias current, and stays at the same level with respect to the peak power from about 20 W to full power; but at the same time the low order intermodulation changes drastically. At a power level of about 1 W the FT1000D spectrum looks like Figure 31. Note that the third order intermodulation product is only about 22 dB below the peak power. This is a very significant distortion of the signal, well visible in the time domain as one can see on the oscilloscope trace in Figure 32. At the zero crossings, the envelope should have its steepest slopes, but as can be seen in Figure 32, the slope is only about 50% of its correct value which means that the amplifier gain is about 6 dB lower than it should be at output voltages about 20 dB below a power level of 1 W. This kind of distortion is commonly referred to as cross-over distortion since it is equivalent to cross-over distortion in hi-fi amplifiers where the name is fully appropriate.


Figure 29: Standard two-tone test for the FT1000D. The tones are 700 and 1900 Hz.


Figure 30: Slightly modified two-tone test for the FT1000D. The tones are 400 and 2400 Hz. The amplitude ratio is adjusted for worst high order intermodulation.


Figure 31: Two-tone test for the FT1000D at about 1 W peak power. The tones are 700 and 1900 Hz.


Figure 32: Two-tone test for the FT1000D at about 1 W peak power. Same signal as in Figure 31, oscilloscope trace of the 14 MHz RF signal

Conclusions and discussion

Testing transmitters is a far more complicated task than testing receivers. It is complicated in the sense that it is very difficult to set up a standardised test that has a chance to be generally accepted, and that would be relevant as a figure of merit for the spectral purity of a modulated transmitter.

Personally I think that excessive high order intermodulation is a direct consequence of the standardised two-tone test, because of the unbalanced emphasis that it gives to the lower (3rd and 5th) orders. The relatively low level of the third order intermodulation visible in the standardised two-tone test may well be a consequence of design engineers tweaking the bias current of the PA and perhaps the driver stages for optimum 3rd and 5th order performance, without regard to any other consequences. The normal 3rd order intermodulation can be described as loss of gain at maximum power, as the envelope is flattened slightly at the maximum power. By deliberately setting too low a bias current to create a loss of gain at the zero crossings as well, one can add another 3rd order intermodulation component that is in antiphase and thus reduces the total 3rd order intermodulation. Such techniques are well known, and often used to take advantage of rigid type acceptance test protocols – but the adverse consequences for wideband splatter are visible as increased levels of higher order intermodulation, even in the standard two-tone test. If the FT1000D had been designed to produce good results in the peak hold spectrum, the bias current would have been just a little higher. The third order intermodulation in the two-tone test would have been a little higher too, but the higher order components would have been much lower... and that is what matters most to other band users. I have been told that the FT1000D is known to produce very clean SSB signals on the bands – “one of the best rigs”. Knowing about the cross-over distortion, amplifier noise and ALC modulation from which it suffers, and how easy it could have been to eliminate all these problems at the development stage, the conclusion is that the current state of the art in amateur radio transmitters is highly unsatisfactory. Bad design is not limited to careless keying.

Besides the test of the purity of modulated emissions, a product review should also include a measurement of the sideband noise of the unmodulated carrier since it gives interesting information about the quality of the frequency generating circuits. The levels of the noise sidebands are easily measured with good accuracy using standard instruments and a notch filter. It is not safe to assume that the reciprocal mixing test in RX mode tells us everything; the TX signal path is different so a separate test is needed, and a comparison with the two signal dynamic range of the receiver may give interesting information. In fact it is quite common for transmitters to be much noisier than receivers, and most often this is due to silly design errors that could be easily rectified. The main requirement now is to escape from the fixation on receiver performance – that problem is now essentially solved [2] – and begin to give transmitter performance the share of attention that it deserves.

[1] Leif Asbrink, SM5BSZ, Receiver Dynamic Range, DUBUS 4/2003 p9-39 and DUBUS Book TECHNIK VI, p348-378. Also see http://www.sm5bsz.com/dynrange/rig_compare.htm and links from there.

[2] Peter E Chadwick, G3RZP, HF Receiver Dynamic Range: How Much Do We Need? QEX May/June 2002, p 36-41.

[3] http://www.sm5bsz.com/linuxdsp/linrad.htm

[4] Mike Gruber, WA1SVF, Improved Transmitted Composite-Noise Data Presentation. QST Feb 1995 p 59.

[5] http://www.sm5bsz.com/linuxdsp/optrx.htm

[6] Doug Smith, KF6DX, On the Occupied Bandwidth of CW Emissions. http://www.doug-smith.net/downloads.htm There is a copy of this article at the SM5BSZ home page: http://www.sm5bsz.com/others/occbw.htm

[7] The ARRL Handbook 1994. Fig. 11 on page 9-9.

[8] Kevin Schmidt, W9CF, Spectral Analysis of a CW Keying Pulse http://fermi.la.asu.edu/w9cf/ There is a copy of this article at the SM5BSZ home page: http://www.sm5bsz.com/others/click.pdf

[9] http://www.w8ji.com/keyclicks.htm and http://www.w8ji.com/keyclick_mp.htm

[10] http://www.qsl.net/n1eu/Yaesu/MPclicks.htm

[11] http://www.qth.com/inrad/kits.htm

[12] http://www.sm5bsz.com/dynrange/alc.htm