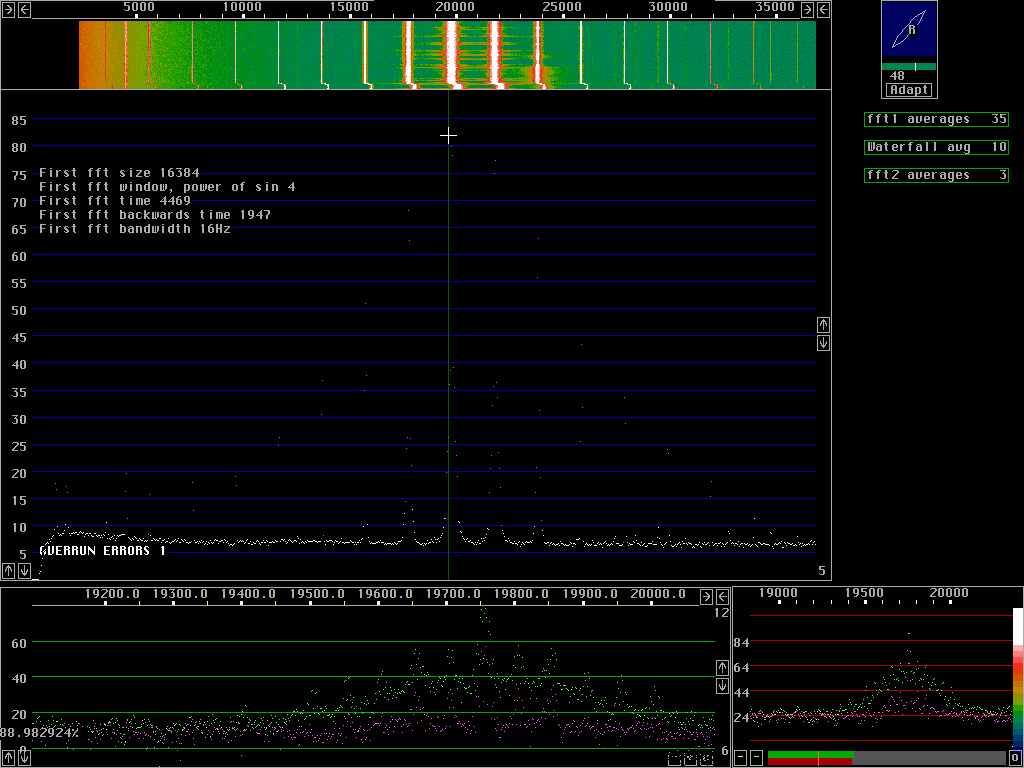
The information on this page is valid only if the second fft is enabledThe first fft setup affects receiver dynamic rangeThis page shows some screen dumps with the signal from a AM modulated signal generator (old style, vacuum tubes). Fig 1 shows what the signal really looks like. The processing is with 16384 points for both the first and the second fft, with a sin to power 4 window for the first fft and a sin squared window for the second.The high resolution graph shows the second fft with one pixel per fft bin separated into the polarisations specified by the polarisation graph. Nearly linear polarisation at an angle of 48 degrees, slightly elliptic right hand. The signal from the signal generator is fed to both channels of the receiver with slightly different cable lengths, that is why the polarisation is slightly elliptic. The waterfall graph of fig. 1 does not show more spurs than those visible in the first fft graph so they originate in the analog hardware. A synthetiser of modest purity was used as a local oscillator.
|
|
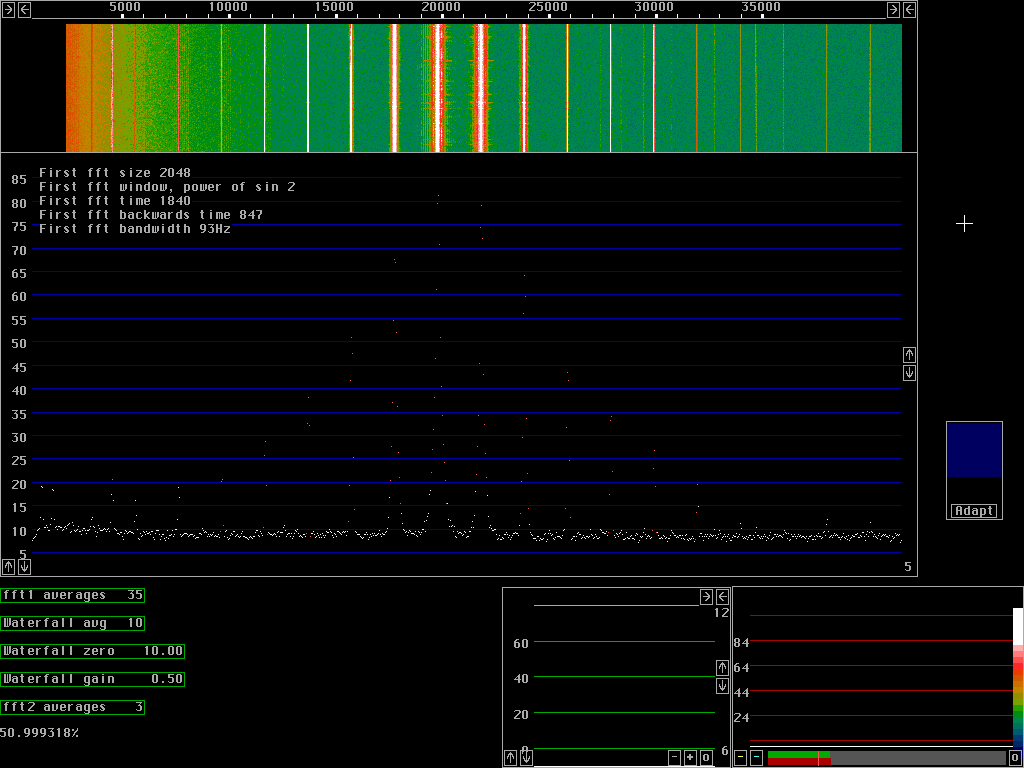
Figure 2 shows what happens when inadequate processing is performed by the first fft. The reason for the spurs is that sucessive back transforms do not fit to each other. The second fft runs with a much larger transform size, 8192 points in fig 2 as in all other screen dumps except fig.1. The mismatch between transforms create transients that form the sidebands clearly visible in fig 2. In real life it is not as bad as it looks. A signal 70dB above the noise floor will typically be a few kHz wide anyway so some extra interference close to it might not make much of a difference.
|

|
There are two ways to get rid of the sidebands around strong
signals.
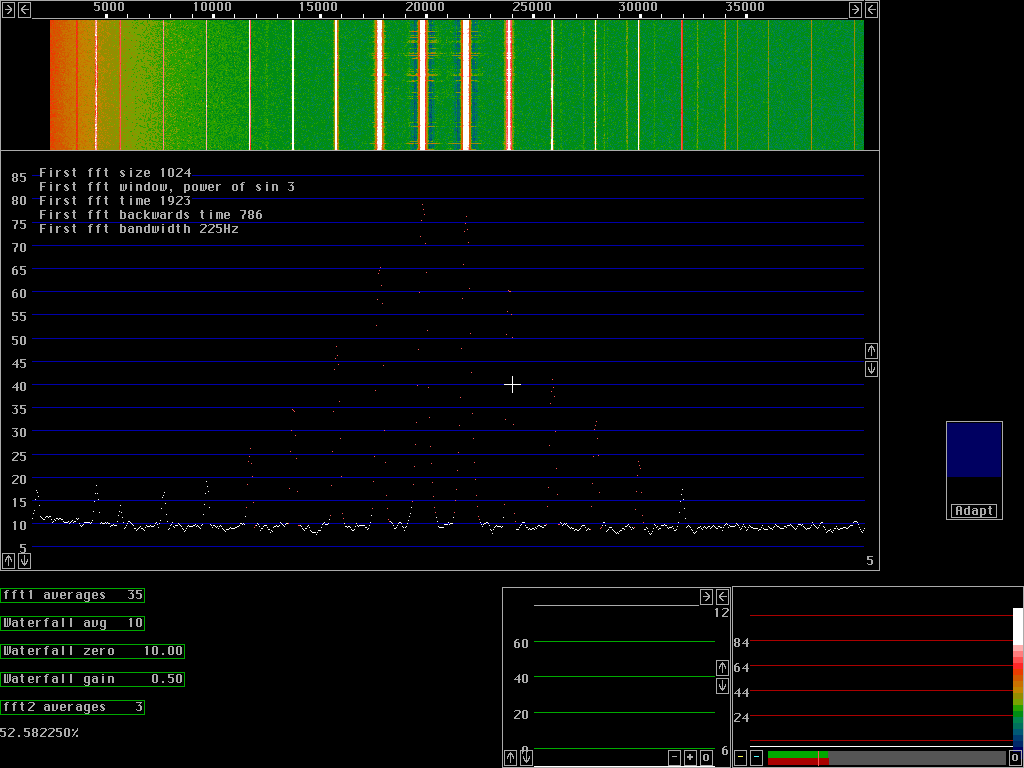
Just by increasing the size of the first fft one can make transients occur less frequently, with less total energy in the sidebands as a consequence. By use of a better window one can remove the transients inherent in the transform itself that arises from the matching of the ends of each transform. This way energy belonging to the strong sine wave will not be distributed over many fft bins. Fig. 3 shows the performance with 1024 fft and sin squared windows. This level of processing will be adequate in most situations although the discontinuity spurs are still visible. The 1024 sin squared window forward plus backward transform use 16.06 + 6.90 = 22.96% of the total available time. |

| Doubling the transform size to 2048, keeping the sine squared window increases the processing time to 26.61% and practically eliminates the transient sidebands. This is shown in fig. 4. |
|
As an alternative, the window can be improved.
Figure 5 shows a 1024 fft with a sin to power 3 window.
The transforms are spaced closer in time so they join each
other at a point where the window is about -3dB.
for this reason and because the window has to be compensated
for in the back transform the time increases more
this way as compared to the doubling of the transform size
but the difference is small.
Note that the AGC action can be seen in fig 5. The blue regions close to the strongest spectral lines indicate a lower signal level despite the hum and noise sidebands of the signal itself. |
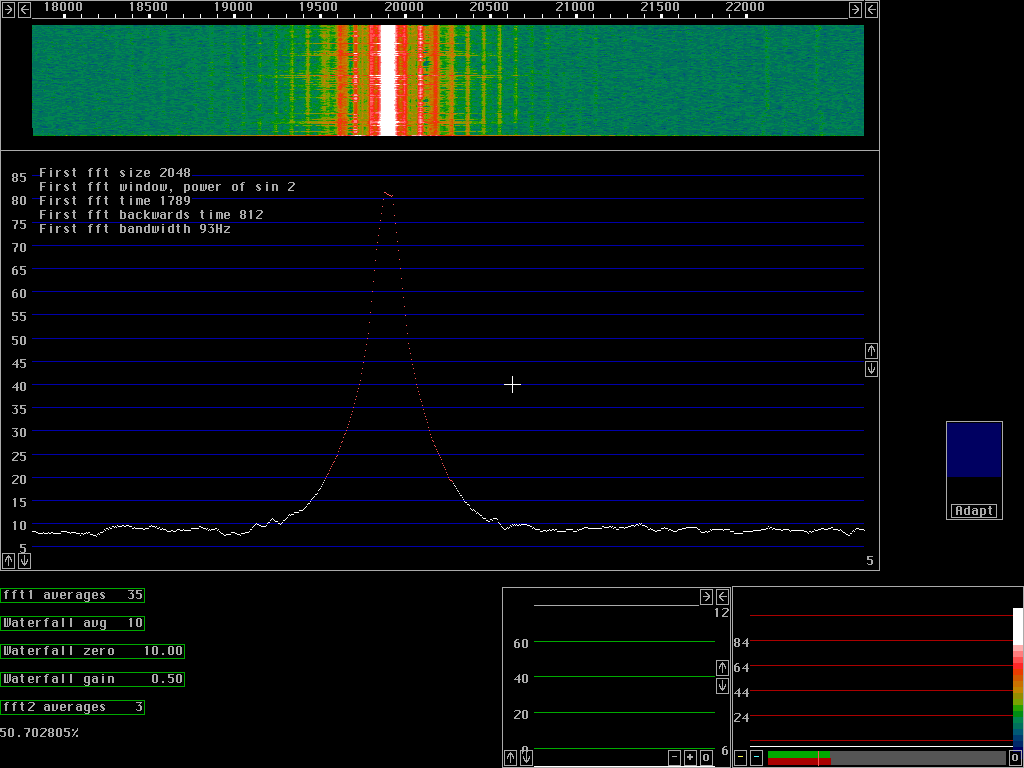
Suggested parameters for the first fftFrom an inspection of fig. 4 and 5 one would conclude that they are both equally good. This is not really the case as one can see from a comparison between fig. 6 and 7. Both these figures show a zoom view on the signal with modulation switched off. It is quite clear that improving the window is better than increasing the transform size.
|
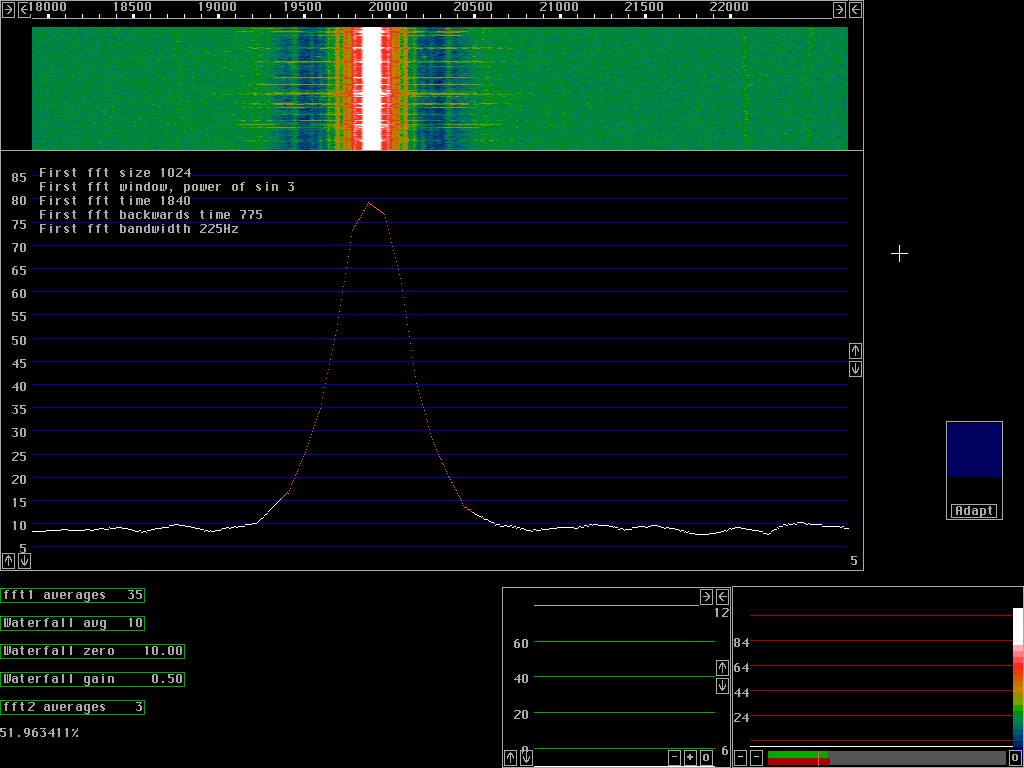
|
All the figures 1 to 7 were produced with the first fft running
in its simplest implementation, vers 0.
The Linux pc radio using Delta44 at 96kHz to provide 90kHz bandwidth, when run on a Pentium III, can well use the parameters demonstrated in fig.8. Using the SIMD instructions of Pentium III (fft1 version 5) the total time for forwards and backwards transformation is 23.25% on a 650MHz Coppermine. Note that the sidebands visible in fig. 8 are the 50Hz hum sidebands of the signal generator, not a processing error. |
