AMPLIFIER NOISE TEMPERATURES

Chuck MacCluer W8MQW 1/9/97

Thermal noise: A body at absolute temperature T (in degrees Kelvin) will emit electromagnetic waves at a power level that is for practical matters constant over all radio frequencies, namely at kT Watts/Hz where k is Boltzmann's constant

k = 1.38 x 10^-23 J/K.

Amplifier noise: Let us think of applying wideband noise power P at kT Watts per Hz to an ideal amplifier of gain G:

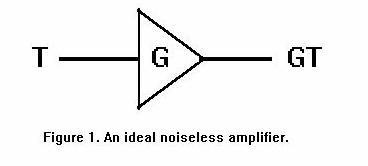
We agree that the above diagram means that when we apply a 1 Hz wide input signal of power P = kT to the amplifier, we obtain a 1 Hz wide output power of Po = GkT.

But a realworld amplifier has internal sources of noise generation---see 1997 ARRL Handbook, p.17-4. Thus the actual situation is that the output power is increased by the internal noise:

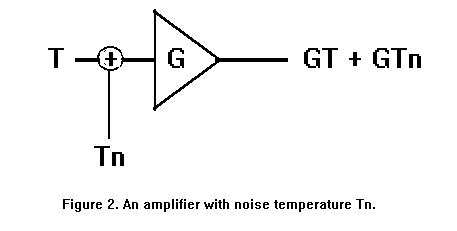
Tn is called the noise temperature of the amplifier.

This noise temperature Tn is found by toggling a source with known on and off temperatures T, and measuring the two resulting levels of output power. Click for the details.

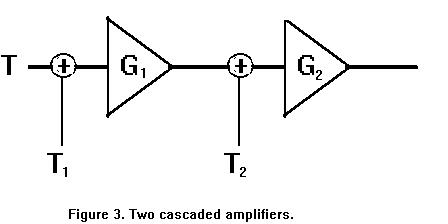
In cascade: Suppose we cascade two real-world amplifiers of gain G1, G2 and noise temperatures T1 and T2:

The power at the output of the first amplifier G1(T1+T) is added to the noise power of the second, and then amplified, to yield

G2(T2 + G1(T1+T)) = G2G1(T1 + T2/G1 + T).

That is, the two amplifiers cascaded are equivalent to a single amplifier of gain G1G2:

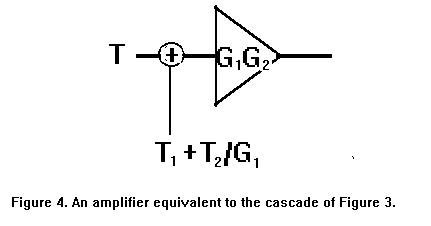
of noise temperature Tn = T1 + T2/G1.

Summary: The noise temperature Tn of the two amplifiers in cascade is the noise temperature of the first plus the noise temperature of the second divided by the gain of the first:

Tn = T1 + T2/G1.

Thus the gain of the first amplifier `washes out' the noise of second stage.

Example 1: The first amplifier has a gain of G1=16 (12 dB) and a noise temperature of 28 K. The second amplifier has the shameful noise temperature 200 K. But the combined pair has a respectable noise temperature of 28 + 200/16 = 40.5 K.

Example 2: A length of coax cable with a loss of 1 dB at the frequency of interest is followed by a low noise preamp of noise temperature 28 K. What is the noise temperature of the combined system?

Think of the coax as an amplifier of gain -1dB, i.e., G1 = 0.79. Assuming the coax is more or less at room temperature 290 K, attach an infinitely long piece of the same type coax also at room temperature to the input of this `amplifier.' The output and input temperatures must both be 290 K since they are both infinite lines. Thus the short piece of coax must have noise temperature Tc where

G1 (290 + Tc) = 290,

i.e.,

Tc = 290/0.79 - 290 = 77 K.

This means the short coax followed by the low noise amplifier has nearly unusable noise temperature of

Tc + 28/0.79 = 113 K.

This is why preamplifiers are mastmounted for weak signal work. Even short runs of coax preceding the low noise amplifier (LNA) severely degrade reception sensitivity. In EME, a second preamplifier will be often installed at the tower to wash out the noise induced by the long run of coax to the receiver inside.

Conversion to dB: In less demanding situations, amplifiers are rated by a quantity called the noise factor F of the amplifier. One assumes the amplifier is seeing room temperature T = 290 K noise power as input---see Figure 2. Then the noise factor F is the ratio of actual output noise over ideal output noise power:

F = G(Tn + T)/GT = (Tn + 290)/290 = Tn/290 + 1,

i.e.,

Tn = 290(F - 1).

The noise figure f is the equivalent in dB:

f = 10 log F.

Here is a conversion table.

Example 1: An amplifier has noise temperature Tn = 60 K. Thus its noise factor

F = 1 + Tn/290 = 1.21

and noise figure

f = 10 log F = 0.82 dB.

Example 2: An amplifier has noise figure f = 1.5 dB. Then its noise temperature Tn is

Tn = 290(F-1) = 290(10^(f/10) - 1) = 120 K.

To reach the author's homepage click on W8MQW . The author welcomes comments via email.