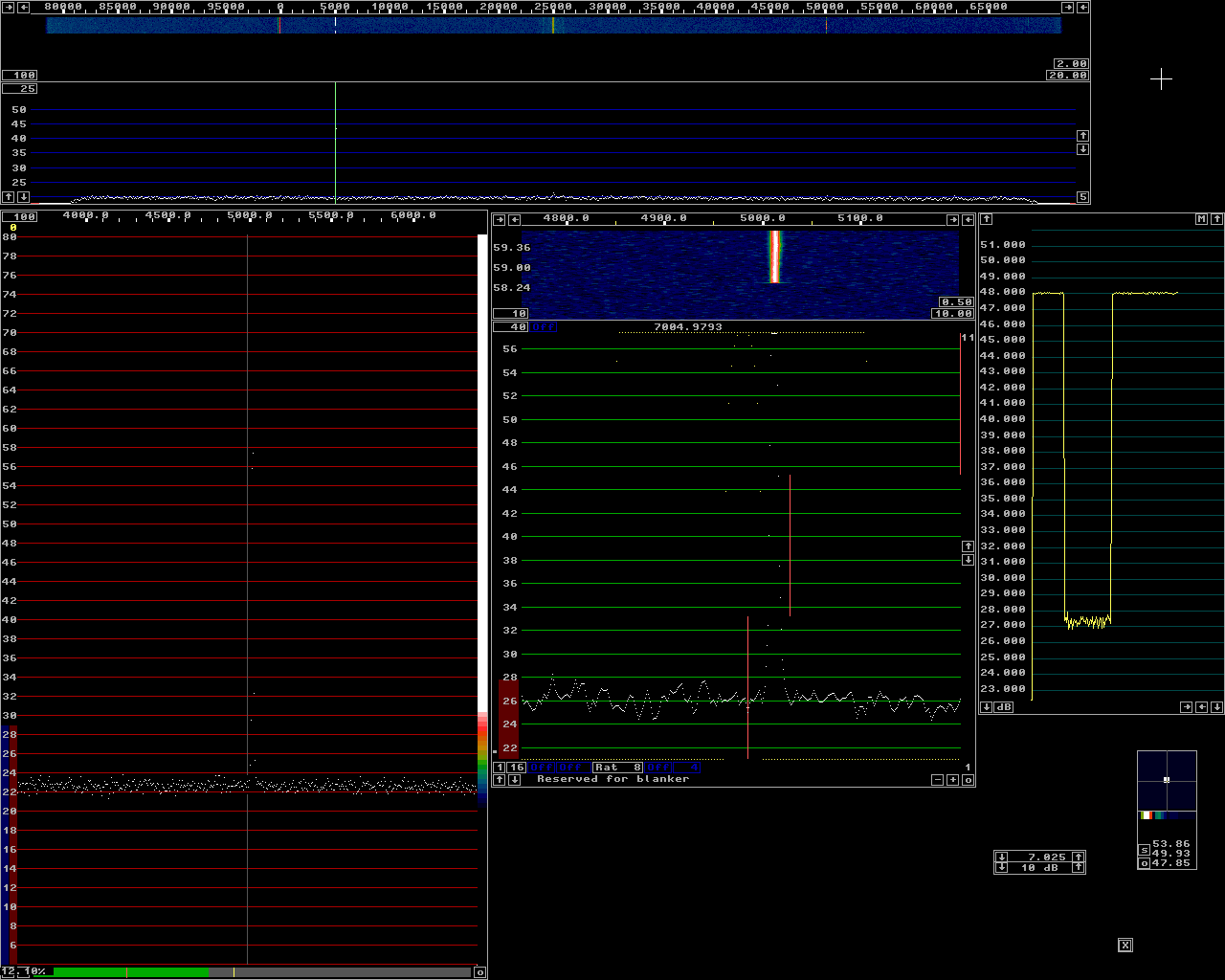
Fig 1.Level -65 dBm. The baseband filter is set to 250 Hz and the S-meter graph shows S/N=20.7 dB.
|
When searching for weak signals on VHF and UHF bands it
is often useful to monitor rather wide frequency bands.
The WSE units allow monitoring about 92 kHz but when the
bandwidth of the FFT is set to match the bandwidth of the
expected weak signal one would need 32768 point FFTs when
searching for JT65 signals with a windowed FFT.
Obviously it would be possible to draw 32 waterfall diagrams
above each other on the screen, allowing each one to cover
about 2.8 kHz.
There is however another option available.
By averaging the large transform over a long time, something like 100 transforms, the noise floor can be made very flat. Then the difference between the strongest out of e.g.32 points will not differ much from the RMS average those points and therefore the increase of the noise floor caused by picking the strongest point rather than the rms value becomes small. When using Linrad for finding JT65 signals in a 92 kHz wide spectrum with WSE units and a Delta 44 sampling at 96 kHz are: FFT1 bandwidth = 200 Hz FFT1 window = sine to power of 3 FFT2 bandwidth factor = 24 FFT2 window = sine The number of averages for the waterfall should be set to 100 for each line in the waterfall to represent the average over 10 seconds. These parameters give a second fft bandwidth of about 8 Hz which is a little more than optimum for JT65. The loss is very small however because if the bandwidth were reduced to 4 Hz for a 3 dB S/N improvement, the number of averages would have to be reduced to 50 to still have 10 seconds for each line. The reduced averaging reduces the advantage to 1.5 dB. The loss in picking the strongest point out of twice as many less well averaged data points for the noise floor reduces the advantage of 4 Hz bandwidth to about 1 dB. In case the signal drifts by more than about 2 Hz during 10 seconds the advantage of narrower bandwidth becomes even less. With these parameters the delay from antenna to loudspeaker is about 0.35 seconds which should allow normal operation of wsjt in another computer on the loudspeaker output from Linrad. To evaluate the detect threshold with the parameters suggested above a signal generator (HP8657B) was connected to a preamplifier through attenuators with a total attenuation of 59 dB. The output of the preamplifier was connected to a RXHFA followed by the other WSE units feeding a Delta44 soundcard. The purpose of the preamplifier is to produce a flat noise floor. The Linrad calibration procedure ensures flat gain over the entire frequency range. The noise contribution from the Delta 44 is however a significant contribution to the noise floor that varies strongly with frequency and therefore the noise floor will not be flat unless the preamplifier is inserted to give a system noise figure that does not vary with frequency. The noise floor has to be flat within about 0.1 dB for the high gains needed in the waterfall colour scales when averaging 100 times. Figure 1 shows the Linrad screen when the signal generator is set to -65 dBm. The baseband filter is set to 250 Hz. The generator is keyed on/off and the S-meter graph shows that S/N=20.7 dB. (at this high level (S+N)/N = S/N) Figure 2 shows the Linrad screen with the generator set to -70 dBm. (S+N)/N is 15.8 dB which means that S/N is 15.9 dB. To produce S/N = 0 dB in a bandwidth of 2.5 kHz the generator would have to be set to -76 dBm. This is the zero level in the "JT65 scale" for the setup on this page. In figure 2 S/N in the high resolution graph is 29.5 dB. Thi signal is right between two bins in the second FFT. If it had been centered on one bin it would have been 2 dB stronger for an S/N of 31.5 dB. This means that S/N is 15.6 dB better (36 times) in the high resolution graph compared to 250 Hz bandwidth and therefore we may conclude that the equivalent noise bandwidth of the second fft is 250/36 = 7 Hz in reasonable agreement with the 8.78 Hz given by Linrad. (The formula producing this value is based on a guess with unknown accuracy.) Figures 3 to 5 show similar screens with the level set to -75 -80 and -85 dBm respectively. They are all consistent with -76 dBm as the zero point for the JT65 scale. Figures 6 to 9 show screens at -90, -95, -100 and -105 dBm respectively. Figure 9 has full gain, 20, in the colour scale for the main waterfall. The signal is very well visible but the colour is not white more than about 50% of the time. Figure 10 shows the screen at -107 dBm corresponding to -31 dB on the JT65 scale. The signal is visible, but only about 50% of the time. If it had been a real JT65 signal which is absent 58% of the time it might well have been invisible, but the chance of detecting it in a 10 minute period, as much as shown in the main waterfall of figure 10 is not too bad. Figures 11 to 14 show screens with the signal level lowered in 2 dB steps. The signal is completely invisible in the main waterfall but it can be seen in the baseband waterfall which has a sampling speed of 6 kHz and an FFT size of 16384 with a sine squared window. The resolution bandwidth is 0.7 Hz which is the narrowest bandwidth compatible to the stability of the equipment. The purpose of figures 11 to 14 is to show that the threshold level, about -31 dB on the JT65 scale for detection in the main waterfall is not incorrect due to leakage of signals outside the attenuators. |

Fig 1.Level -65 dBm. The baseband filter is set to 250 Hz and the S-meter graph shows S/N=20.7 dB. |
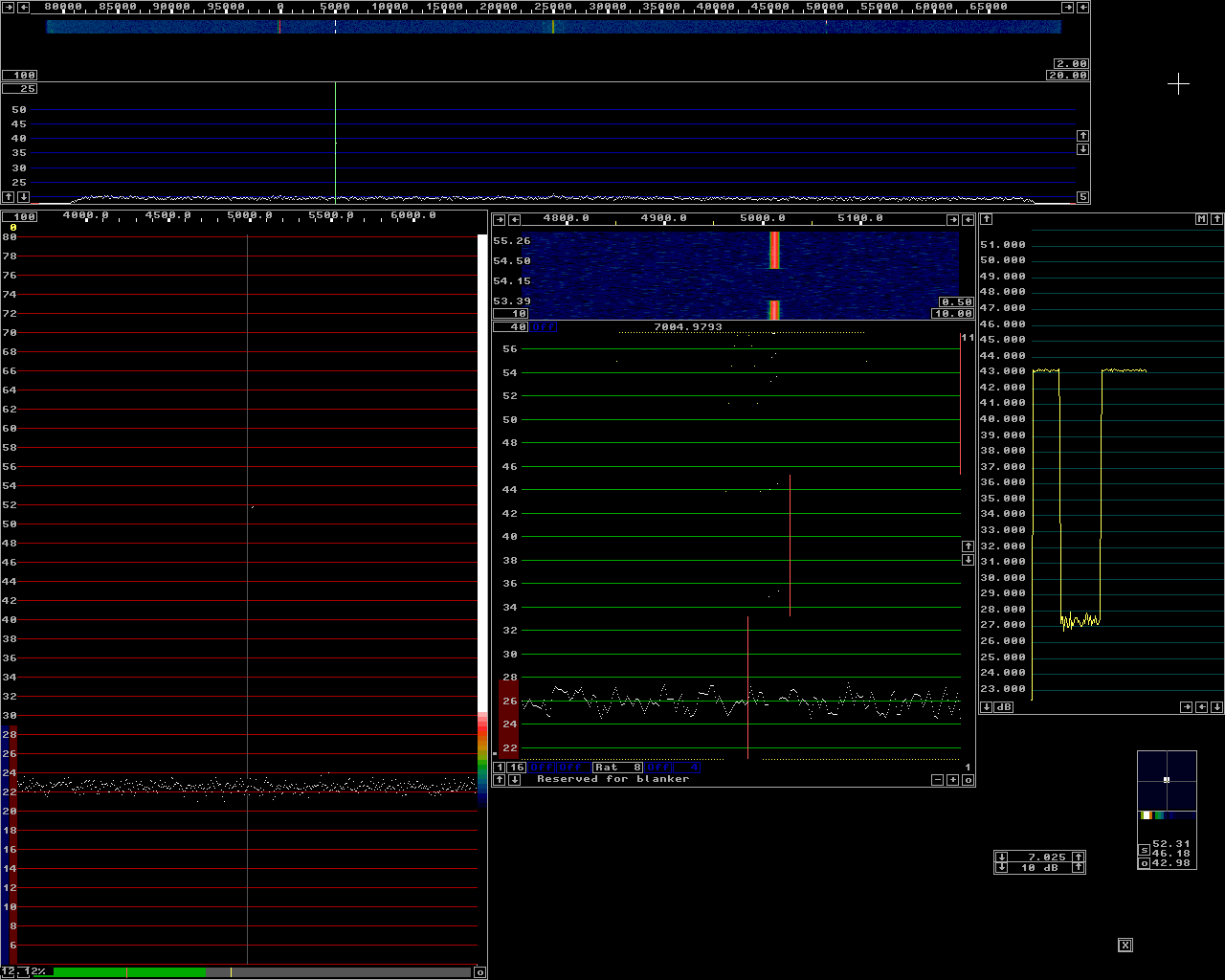
Fig 2.Level -70 dBm. The baseband filter is set to 250 Hz and the S-meter graph shows (S+N)/N=15.8 dB. |
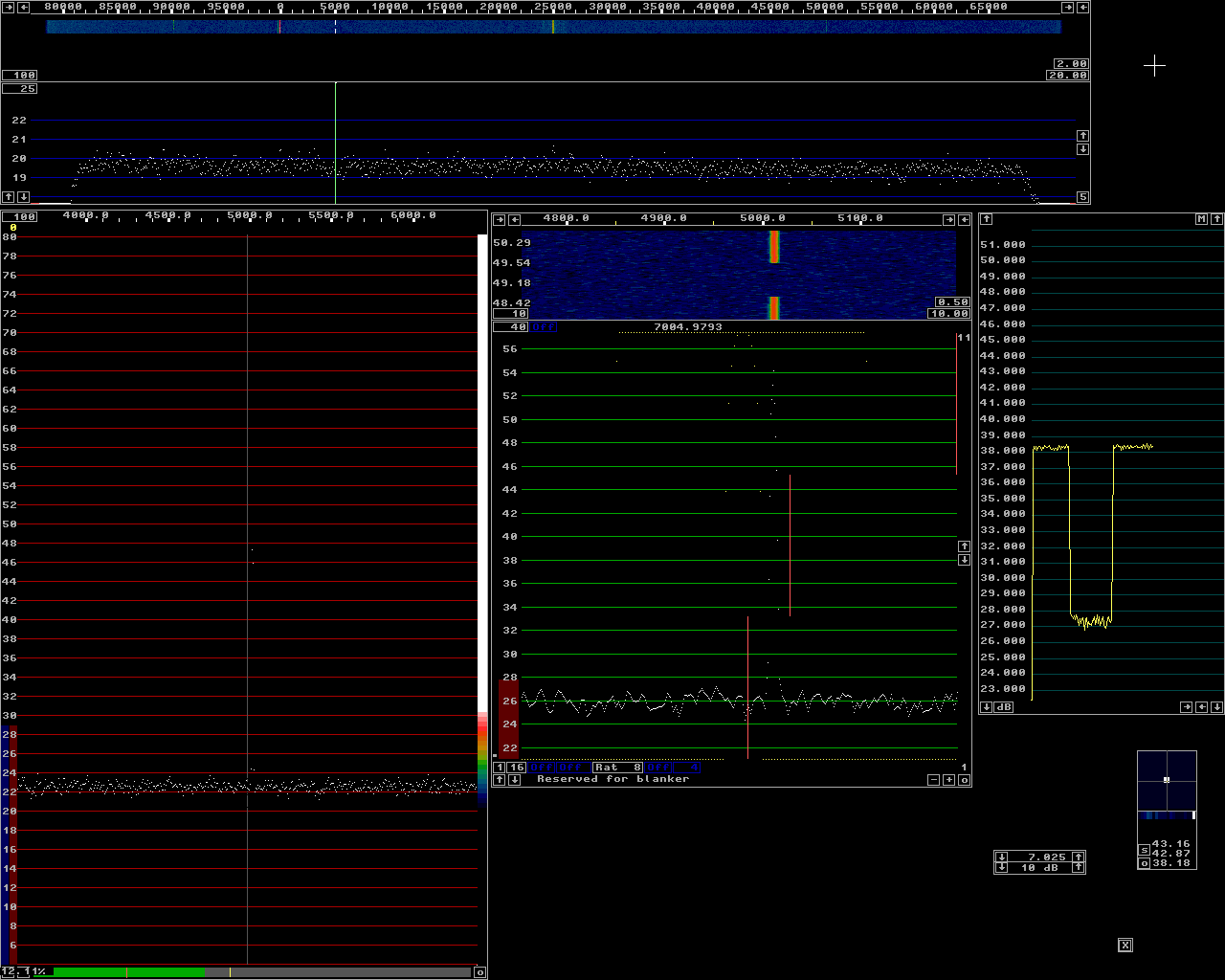
Fig 3.Level -75 dBm. The baseband filter is set to 250 Hz and the S-meter graph shows (S+N)/N=11.0 dB. |
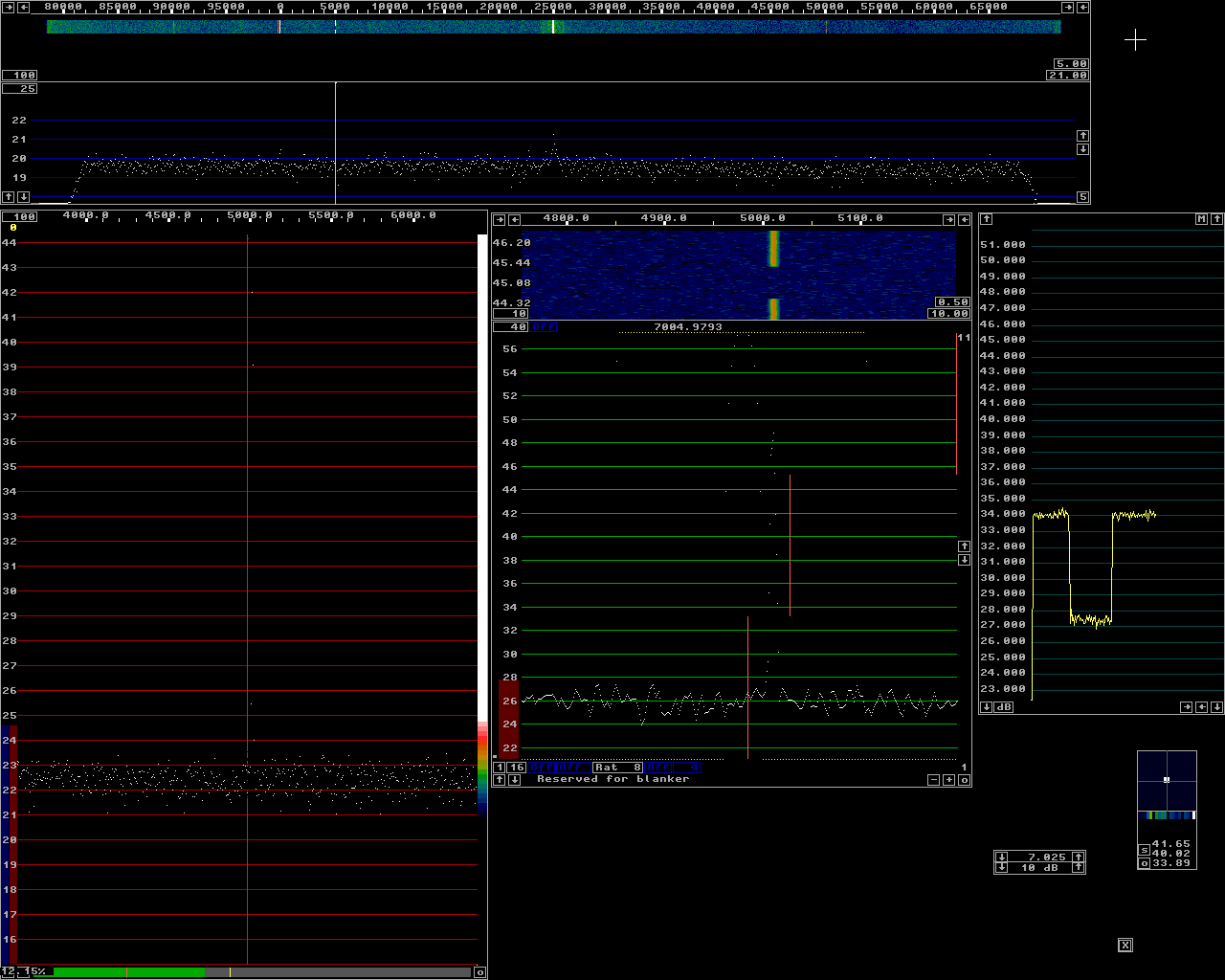
Fig 4.Level -80 dBm. The baseband filter is set to 250 Hz and the S-meter graph shows (S+N)/N=6.7 dB. |

Fig 5.Level -85 dBm. The baseband filter is set to 250 Hz and the S-meter graph shows (S+N)/N=3.5 dB. |
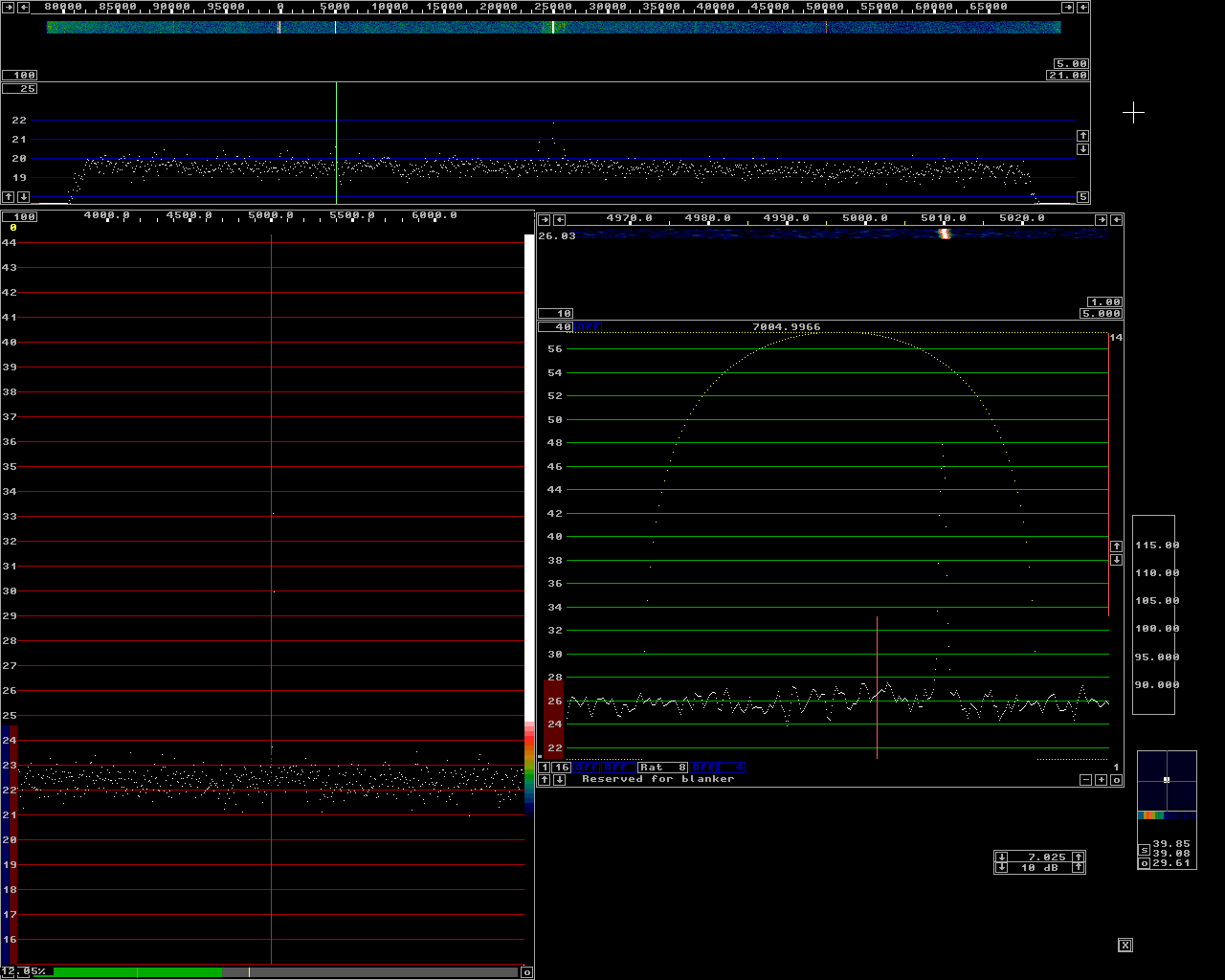
Fig 6.Level -90 dBm corresponding to -14 dB in the JT65 scale. |

Fig 7.Level -95 dBm corresponding to -19 dB in the JT65 scale. |
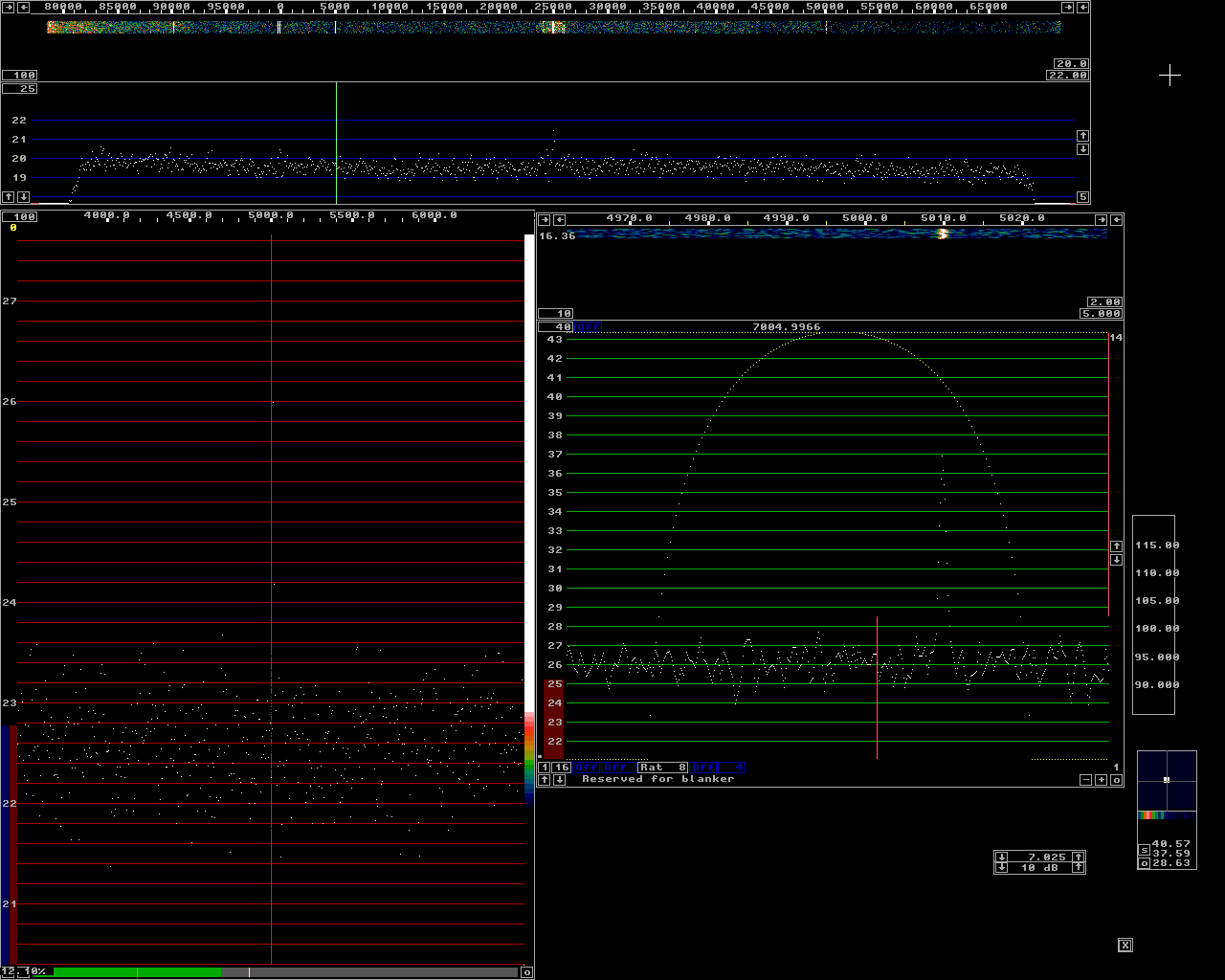
Fig 8.Level -100 dBm corresponding to -24 dB in the JT65 scale. |
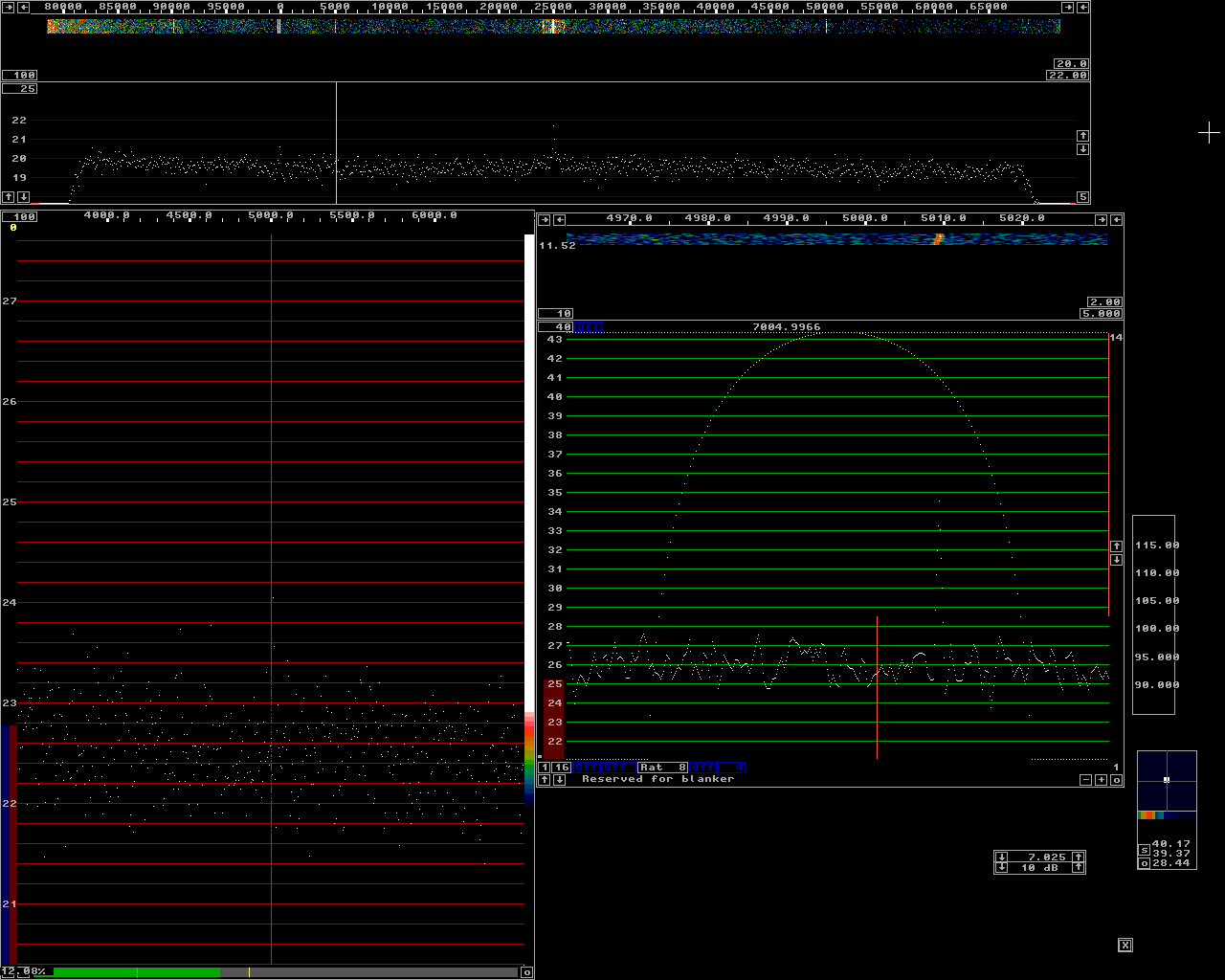
Fig 9.Level -105 dBm corresponding to -29 dB in the JT65 scale. |

Fig 10.Level -107 dBm corresponding to -31 dB in the JT65 scale. |
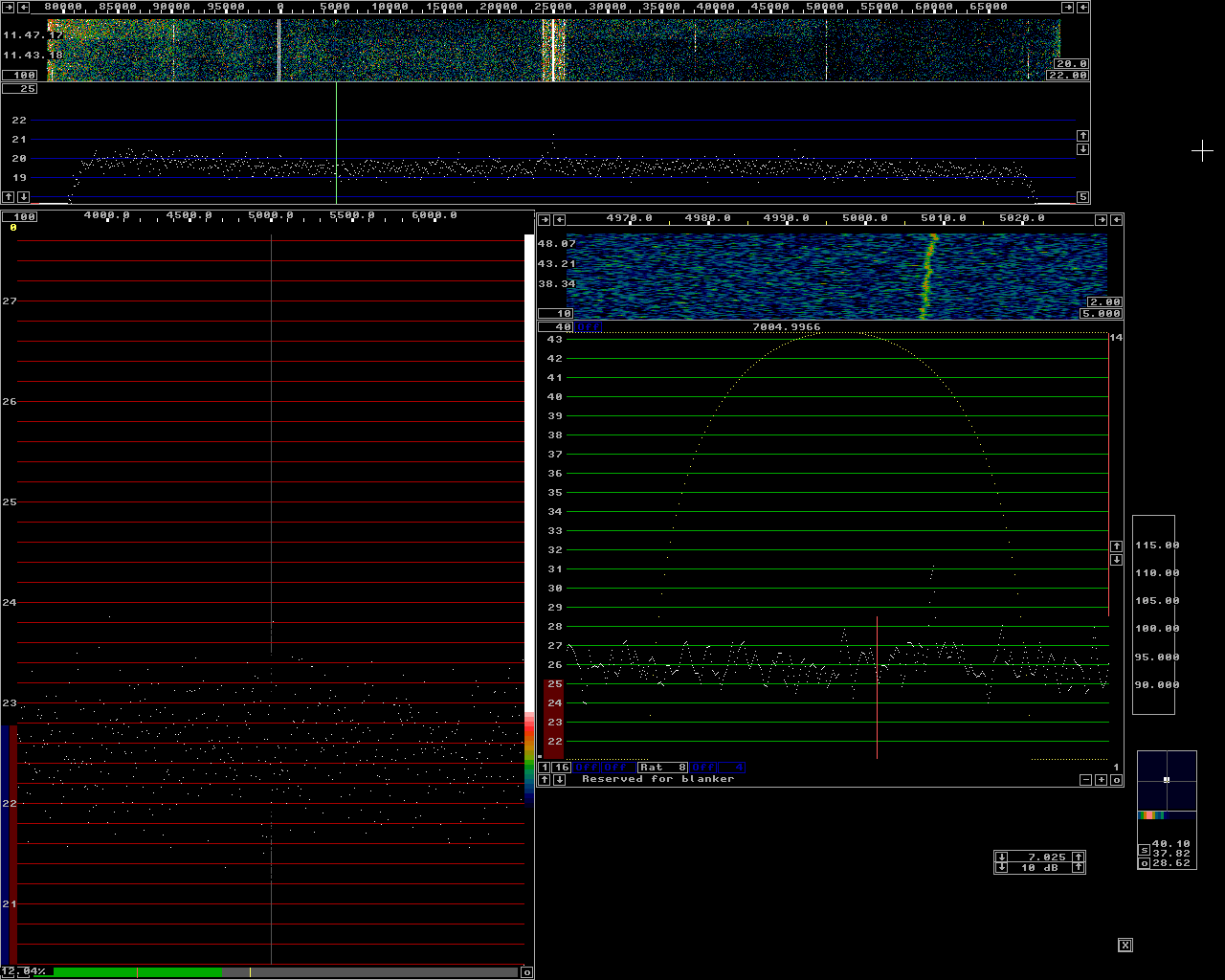
Fig 11.Level -109 dBm corresponding to -33 dB in the JT65 scale. The signal can not be seen at all in the main waterfall. |
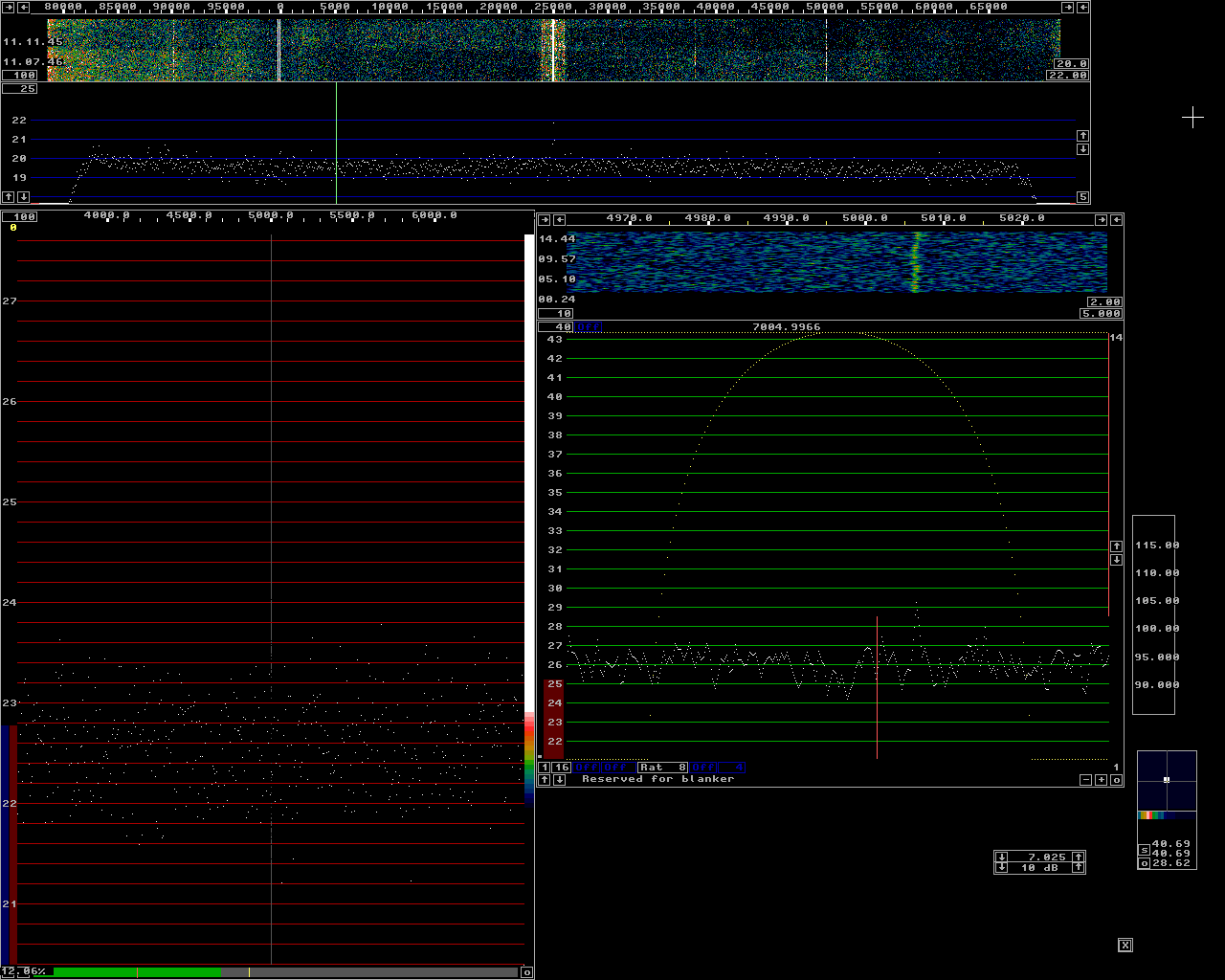
Fig 12.Level -111 dBm. |
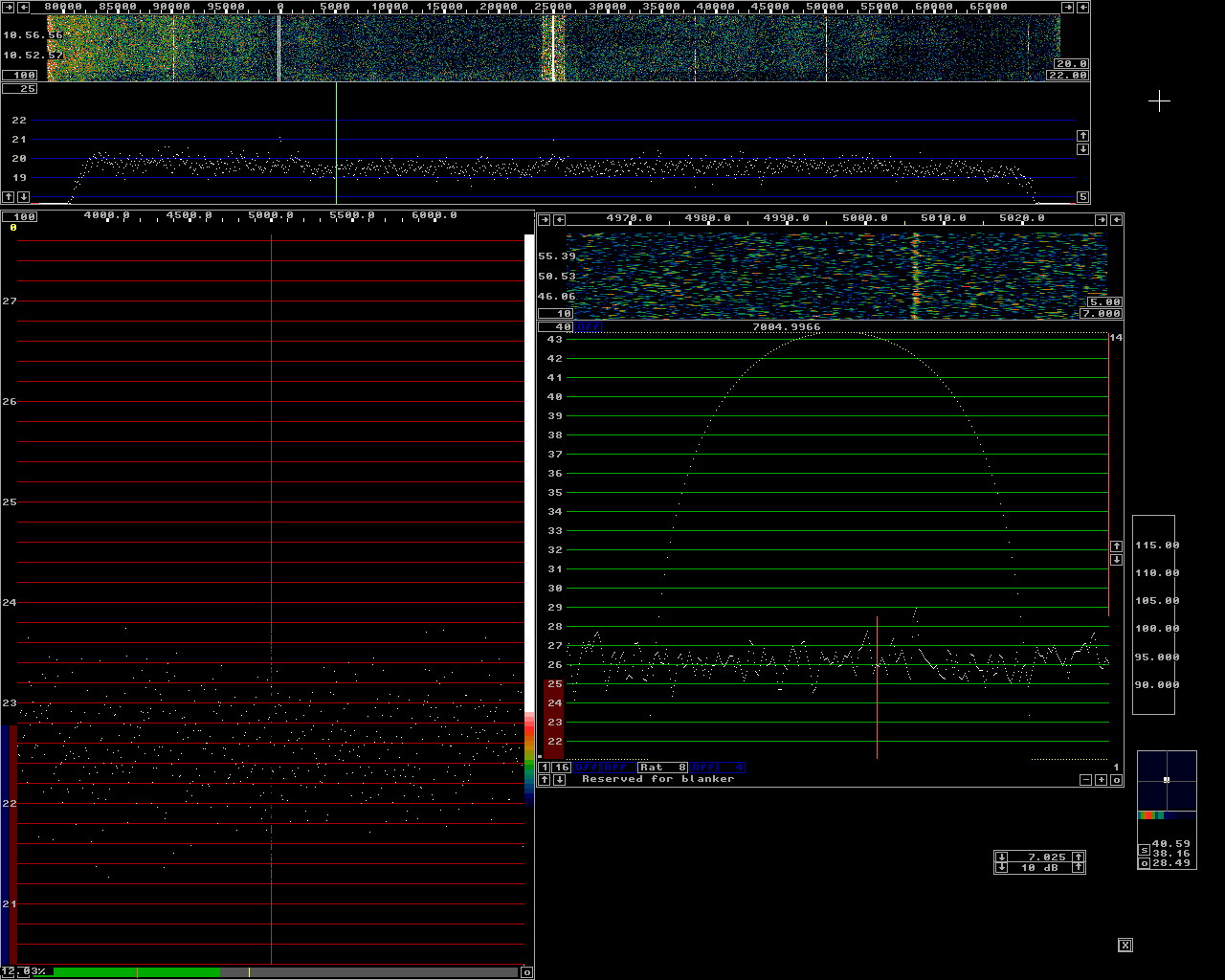
Fig 13.Level -113 dBm. |
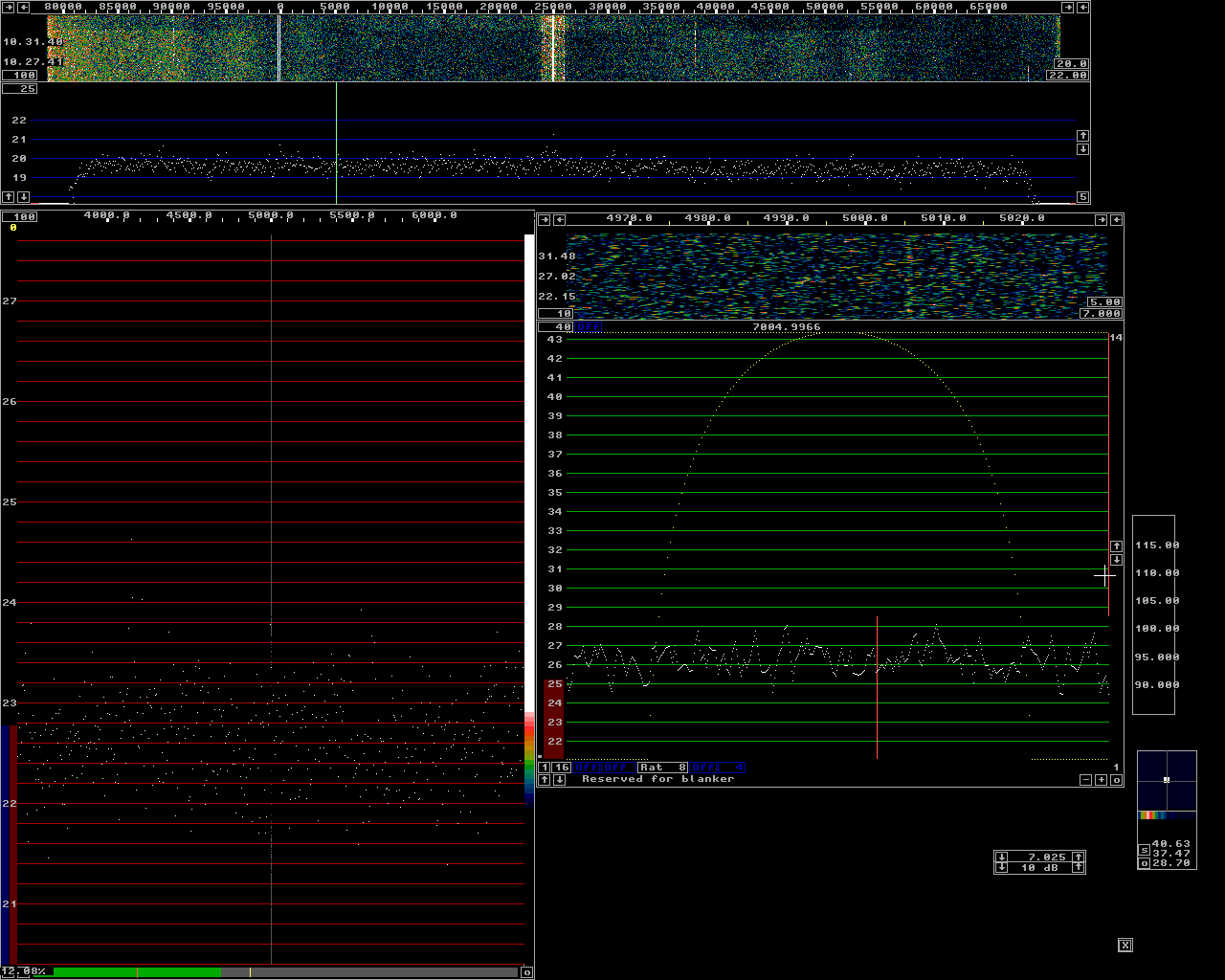
Fig 14.Level -115 dBm. |
|
To SM 5 BSZ Main Page |