
Phase noise measurementsBackground.This article is the result of a project that I started after the Scandinavian VHF Meeting in Knottebo 2009. I had brought some equipment for the evaluation of amateur transceivers and one of the units was a crystal oscillator that I had long ago measured to give a sideband noise level of -169 dBc/Hz.Rohde & Schwarz Sweden was present at the meeting with some test equipment so I decided to check my low noise oscillator. The result was surprising. See figure 1. | ||

| ||
|
Figure 1. The "-169 dBc" oscillator measured at Knottebo
Jun 13 2009. The result at a frequency separation of 10 kHz with the FSUP was -175.8 dBc/Hz, nearly 4 dB better than expected under the assumption that the oscillator has equal amounts of phase noise and amplitude noise. Back home I repeated my measurements and could conclude that something was definitely wrong. I decided to try to find out what was the the cause of the discrepancy and to that end I designed some more oscillators which I subsequently brought to R&S in Stocholm for measurement. All the oscillators have a frequency near 14.16 MHz and a power level of about 15 dBm. These are the five oscillators: 1) My old reference oscillator. A low noise crystal oscillator named OLDREF in this article. 2) A low noise wide range VCO An LC oscillator with no fixed C, only capacitance diodes in the LC resonator. It is named VCO in this article. 3) A VCO with a common design error. It is named FM in this article. Very similar to the previous one. This one differs in that the capacitance diode is supplied with the tuning voltage through a 1 megohm resistor rather than through an inductor. This oscillator has high phase noise because the thermal noise of the resistor and the noisy voltage drop due to the diode leakage current produces FM modulation. 4) A crystal oscillator with a common design error. It is a good crystal oscillator followed by a buffer stage that is supplied with +12 volts directly from a 7812 that is decoupled with a 1 uF capacitor only. This oscillator has high AM noise and is named AM in this article. 5) My new reference oscillator. A very low noise crystal oscillator named NEWREF in this article. The Colpitts Oscillator may also be of interest to compare with the five test oscillators. The explanation for the incorrect result at Knottebo turned out to be the presence of overtones. The rest of the article describes the measurements I can do at home and compares them with the results obtained from the Rohde & Schwarz FSUP. Dynamic range limitations.The easiest way to measure sideband noise is to use a receiver or spectrum analyzer to measure the RMS power within a well defined bandwidth. This way one would measure the sum of AM noise and phase noise. I have used a Perseus HF receiver which has a noise floor of about -145 dBc/Hz and it allows the direct measurement of sideband noise down to about -135 dBc/Hz.The dynamic range of the Perseus is good enough to allow direct measurement of the sideband noise of typical amateur radio transmitters like FT-1000D, FT1000MPMV, IC-718, IC-756PROII, IC-7600, IC7800, TS-450S, TS-2000 and others. performance data of modern transceivers. The Perseus is however not good enough to allow direct measurements of the sideband noise levels of the five oscillators in this study. Only no. 2, FM, has a sideband noise level high enough to allow a direct measurement. The direct measurements of sideband noise above about -135 dBc/Hz is uncomplicated because the test object is always connected to one and the same load which has the same impedance for all (relevant) frequencies. Linrad can be used to determine RMS power in a well defined bandwidth. By use of the coherent detector in AM mode one can split the total modulation in two components I and Q where I is the AM noise and Q the phase noise. The use of a notch filter to extend the dynamic range.It is possible to insert a notch filter between the test object and the analyzing receiver (or spectrum analyzer). This way the carrier can be suppressed while the sideband noise is not much affected.Such measurement is made in two steps. In a first measurement the power level of the test object is determined with some suitable attenuators in place to prevent overload. In a second measurement the notch filter is inserted and the attenuators are replaced by low noise amplifiers. The RMS power is then measured at some specific frequency separation. The problem of this method is to accurately determine the shift in the zero point of the dB scales of the two measurements. There are several different ways. The easiest one is to get the carrier level in dBm from a separate measurement using a calibrated power meter of some kind. A spectrum analyzer would typically give the power level within 1 dB. One can then use a noise source to measure the noise figure at the input of the notch filter at the desired frequency separation. The noise floor is then -174 +NF dBm/Hz. Combining the two measurements would give the sideband noise within about 2 dB. Not too bad. Easy to understand and easy to perform, but this measurement is the difference between two absolute measurements so we can do better. We may start with a power measurement having an unknown error X and use it to measure the noise figure. When the same signal is used to measure the sideband noise the error X in the power level will be cancelled by its occurance in the NF value. Normally one would assume that all equipment is 50 ohms, but for high accuracy it is necessary to make sure that the impedance changes that may occur will not affect the measured results. The input impedance of a notch filter is typically very different from 50 ohms. Definitions (for this article): Power level: The power a particular unit would deliver to a load having exactly the nominal impedance (50 ohms.) Noise figure The noise floor in relation to the noise of a room temperature resistor when the source impedance is exactly the nominal impedance (50 ohms.) To perform the measurement a second signal is needed. It should have a much lower power level than the test object but it should be high enough above the noise floor to allow accurate measurement of the power level. The second signal is subsequently used to measure the noise figure. The possible errors are the following. 1) Statistical errors in the determination of the RMS power of the noise floor. 2) Errors in the RMS noise floor caused by an error in the bandwidth. 3) Errors caused by nonlinearities in the A/D converter. 4) Errors caused by impedance errors. 5) Errors caused by mistakes. All these errors should be small. To do the measurements an impedance reference is required. If you do not have professional equipment, build a directional coupler using a ferrite core and a resistor or buy one. Use the directional coupler to to tweak the impedance of the measuring receiver until the return loss is 47 dB or better. (Less than 1% impedance error.) Use it also to tweak the impedance of the signal source used for the NF measurement. I am using exactly 50 ohms (within less than 0.25%) by use of a network analyzer in my measurements to get correct absolute power levels, but for the accuracy of the sideband noise measurements it does not matter. Just use the directional couple to make sure the impedance is exactly the same at those places where I use the network analyzer to set the impedance to 50 ohms. Absolute measurements of power levels.Although not necessary for sideband noise measurements it is interesting to minimize the error X in the power level. There are two ways. One can start from an accurate knowledge of a noise figure or one can start from an accurate power meter. It is interesting to try both ways simultaneously as a consistency check.How do I know to what impedance my old network analyzer should show when it looks into exactly 50 ohms? This link Impedance calibration describes how I did that. This link also explains why the impedance has to be the same in a measurement of power ratios and that the 47 dB return loss requirement gives an uncertainty in a power ratio of 0.028 dB. The test oscillators were measured with an accurate power meter at R&S in Stockholm. After returning home I measured the power levels with the Perseus having attenuators and a PI filter to set the impedance to 50.0 ohms. This configuration is shown in figure 2 and labeled Perseus(A) below. Note that the 50.0 ohms impedance is not at the 10 dB attenuator of the match box shown in figure 2 but at the other end of the cable that was used for these measurement. The same cable was used to check the impedance with the network analyzer and to connect Perseus(B) to the various signal sources. This way I could make sure that all the signal sources were seeing a load of exactly 50 ohms in the measurements. Here are the results:
Unit Pow.meter Perseus(A) diff
(dBm) (dBm) (dBm)
OLDREF 17.396 17.413 -0.017
FM 11.756 11.980 -0.224
VCO 11.727 11.840 -0.113
AM 11.230 11.475 -0.245
average -0.150
Note that the dBm scale of Perseus(A) is arbitrary.
This table establishes how it relate to known power levels.
| ||

| ||
|
Figure 2. Perseus(A) The sensitivity of the Perseus
receiver is reduced by 30 dB and the input impedance at the 10 dB attenuator is exactly 50 ohms resistive.
The matchbox contains a PI filter that allows
fine tuning of the impedance. To establish reference power levels for the future I also measured the signal levels from my five HP 8657 signal generators when set to +10 dBm and -50 dBm dBm with Perseus(A). Still, of course using the same cable and matchbox setting. By correcting the results with -0.150 dBm the average difference between Perseus(A) and the power meterI get values that are probably within 0.1 dB from what I would have seen if I had had access to a power meter at home. Perseus(A)
Gen set to +10 dBm Gen set to -50 dBm
Gen No Measured Corrected Measured Corrected
(dBm) (dBm) (dBm) (dBm)
1 10.300 10.150 -49.548 -49.698
2 9.302 9.152 -50.201 -50.351
3 9.471 9.321 -50.100 -50.251
4 9.870 9.720 -49.927 -50.077
5 9.918 9.769 -49.968 -50.118
The power levels of the HP 8657 generators are probably stable
in time.
The generators have not been calibrated in 10 years and they are
all well within the +/- 1 dB specification.
That is a good reason to believe these generators are stable with time.
The corrected values above will serve as a reference for power levels
in the future.
In a second series of measurements the five HP 8657 generators were measured with Perseus(B) shown in figure 3. Here the sensitivity is about 42 dB better. 30 dB attenuation is replaced by 12 dB gain. | ||

| ||
|
Figure 3. Perseus(B) The sensitivity of the Perseus
receiver is increased by 12 dB by use of two series connected
6 dB amplifiers.
The matchbox contains a PI filter that allows
fine tuning of the impedance. The dBm scale of Perseus(B) is also arbitrary. By measuring the HP generators once more it is possible to find out what the error is and then to use that error to correct the measurements of the generators at -100 dBm: Perseus(B)
Gen set to -50 dBm Gen set to -100 dBm
Gen No True Measured Error Measured Corrected
(dBm) (dBm) (dB) (dBm) (dBm)
1 -49.698 -50.288 -0.590 -100.142 -99.543
2 -50.351 -50.965 -0.614 -100.906 -100.307
3 -50.251 -50.862 -0.611 -100.927 -100.328
4 -50.077 -50.671 -0.594 -100.550 -99.951
5 -50.118 -50.704 -0.586 -100.744 -100.145
average -0.599
These corrected power levels will also be reference power levels
for me to use in the future.
The reference power levels are not produced by sources that
have the correct impedance.
In order to make noise figure measurements a signal source with
the correct impedance and a known power level is needed.
Such a signal is obtained at the other end of the coaxial cable
leaving the HP 8657 shown in figure 4.
| ||

| ||
|
Figure 4. With a T-connector and 820 ohms in parallel
with 10 k ohms ans an inductor of 12 microhenry the impedance
at the other end of the cable is exactly 50.0 ohms.
This is the power source used for noise figure measurements.
When the cable from the power source shown in figure 2 is connected to the cable constituting the 50.0 ohm input of Perseus(B) the observed power level is -101.373 dBm. Adjusting for the error of the arbitrary power scale gives the true power level of this 50 ohm source to -100.77 dBm Noise figure measurements.Besides the two high level 6dB amplifiers shown in figure 2 I brought a simple amplifier with BFR91A to R&S in Stockholm when doing the sideband noise measurements. The three amplifiers labeled A and B for the high level amplifiers and C for the BFR91A were measured with the FSUP and a noise source. The results are shown in figures 5 to 7. | ||

| ||
|
Figure 5. Amplifier A. Gain=6.6 dB and NF=5.0 dB at 14 MHz.
| ||

| ||
|
Figure 6. Amplifier B. Gain=6.6 dB and NF=5.1 dB at 14 MHz.
| ||

| ||
|
Figure 7. Amplifier C. Gain=19.1 dB and NF=3.5 dB at 14 MHz.
Using the known power level of -100.77 dBm established above and a bandwidth of 10 kHz the following signal and noise levels were observed:
Amp N (S+N) (S+N)/N S/N NF R&S
(dBm) (dBm) (dB) (dB) (dB) (dB)
None -124.97 -113.60 11.37 11.04 22.19 22.19
C -121.65 -94.42 27.23 27.23 6.00 6.3
C->B->A -111.04 -81.33 29.71 29.71 3.52 3.75
C->A->B -111.02 -81.32 29.70 29.70 3.53 3.74
A->B->C -108.59 -80.98 27.61 27.61 5.62 5.81
B->A->C -108.61 -80.97 27.64 27.64 5.59 5.87
By use of my old NF meter, a Magnetic 116B with a vacuum tube
noise source model 123-A I could measure the system noise
figure of the configuration C->B->A->Perseus to 3.60 dB.
The specification for the 123-A says that the error is less
than 0.25 dB.
The above measurements give the system noise figures and the last column gives the system noise figure calculated from the FSPU data using standard formulae for cascaded amplifiers under the idealized assumtion that they are perfectly matched to 50 ohms. The noise figure of the configuration C->B->A->Perseus is now evaluated in three totally independent ways. The values are 3.52, 3.60 and 3.75 and they are so close that I can not draw any particular conclusion from them. Composite sideband noiseThe measurement is simple now that I have reliable power references. The old reference oscillator that was measured in Knottebo produces 17.41 dBm in a 50.0 ohm load while the power source shown in figure 3 produces -100.77 dBm in the same 50.0 ohm load.With the configuration Perseus(C) which is shown in figure 8 a load of 50.0 ohms is presented to the test object at a frequency 10 kHz below the oscillator frequency. At the signal frequency VSWR is about 2. For this measurement to be valid it is necessary for the test object to not be affected by the mismatch at the signal frequency. All the test oscillators have builtin class A MOS-FET amplifiers with noiseless feedback that ensure linear operation at VSWR=2. In case the output amplifier were driven into the non-linear region it would be necessary to place a buffer stage between the test object and Perseus(C). | ||

| ||
|
Figure 8. Perseus(C) A receiver configuration
with a notch filter at the input.
3dB attenuator -> match box -> notch filter -> Receiver (NF=3.6 dB) When Perseus(C) was connected to the reference power source -100.77 dBm on 14.1482 MHz the power level -100.73 was observed on the Linrad S-meter. Note that this is an arbitrary result, I had entered a reasonable but not accurate calibration value of 30.000 into the S-meter calibration box in Linrad. With the 50 ohm dummy load the noise floor was -121.80 dBm which means that the noise figure was 22.9 dB on 14.148 MHz. The noise floor was -119.35 dBm with the old reference oscillator which means that the noise from it only lifts the noise floor by 2.45 dB and that there fore the total power of the sideband noise is less than the noise floor associated with NF=22.9 dB. The Linrad screen with the old reference oscillator connected to Perseus(C) is shown in figure 9. | ||

| ||
|
Figure 9. OLDREF connected to Perseus(C).
The composite sideband noise level is evaluated like this: (S+N0)/N0 = 21.07 dB (121.80-100.73) (N1+N0)/N0 = 2.45 dB (121.8-119.35) By converting from dB to linear power scale we get: (S+N0)/N0 = 127.9 (N1+N0)/N0 = 1.757 S/N0 = 126.9 N1/N0 = 0.757 S/N1 = 167.6 (126.9/0.757) When we go back to dB we find S/N1 = 22.23 dB. Since S is -100.77 dBm we have found that N = -123.0 dBm which places the sideband noise at -153.0 dBm/Hz. The power level of OLDREF is +17.41 dBm so the final result is that the composite noise floor, AM noise plus FM noise, is at -170.41 dBc/Hz. To analyze the modulation type, AM or phase noise, one can use the coherent detector in AM mode. This is demonstrated in figure 10. | ||

| ||
|
Figure 10. OLDREF connected to Perseus(C) and
analyzed in the coh 2 mode of the AM detector.
The Coh2 mode in Linrad uses a narrow filter to extract the phase of the carrier. The baseband signal is then produced by a quadrature detector that places I, the amplitude component in channel 1 (left) and the phase component in channel 2 (right). The carrier is very strong compared to the modulation sidebands and therefore a notch is used in the baseband filter to remove the carrier and thereby remove the DC component which would otherwise saturate the I channel. An audio generator connected to a loudspeaker generates vibrations at 16.3 kHz and produces pure FM modulation. The loudspeaker signal is saved to the hard disk at 96 kHz. | ||

| ||
|
Figure 11. The file recorded as shown in figure 10.
The AM modulation is green and the phase modulation magenta
in the baseband graph.
An inspection of figure 11 shows that the phase modulation produced by microphony is present in Q only as expected. The noise in I and Q is equal in amplitude and therefore the final result is this: OLDREF phase noise @10kHz = -173.4 dBc/Hz OLDREF AM noise @10 kHz = -173.4 dBc/Hz This result should be accurate within a few tenths of a dB and the deviation from the measdurement at Knottebo, 2.4 dB, is quite a bit larger than the accuracy specification of the FSUP. New measurements with FSUP.The new measurements were performed with a later model of the FSUP. The phase noise obtained for OLDREF is shown in figure 12. | ||

| ||
|
Figure 12. OLDREF measured with another FSUP
than the one used for figure 1.
The new measurement gives -167.4 dBc/Hz. That is an error of 6 dB and it differs by 8.4 dB from the previous measurement. Something is VERY wrong..... | ||

| ||
|
Figure 13. The spectrum of OLDREF.
Figure 13 shows the spectrum of OLDREF. The third harmonic is suppressed by about 22 dB only. The FSUP manual clearly specifies that "signal harmonics < 30 dBc" is required for the 1 dB measurement accuracy. | ||

| ||
|
Figure 14. The spectrum of OLDREF with a lowpass
filter BLP-15 (Mini-Circuits) added.
When the filtered signal was measured the result was as shown in figure 15. | ||

| ||
|
Figure 15. OLDREF filtered through a low pass filter.
Now the phase noise measurement is ok.
Problem solved!!! ALWAYS READ SPECIFICATIONS CAREFULLY. All subsequent measurements on OLDREF including the power measurements above were made with the low pass filter in place. Note that the power level shown in figure 15 is higher and much closer to the value obtained with the power meter than the values obtained without the filter. VCOThis is a VCO with a coil and a capacitance diode. The control voltage to the capacitance diode is connected through an inductor. At 10 kHz the phase noise is -142.6 dBc/Hz. See figure 16.Since this oscillator is free-running it the phase noise close to the carrier is very strong. It is not possible to analyze the AM and phase noise components separately with a notch filter since the carrier frequency varies over a frequency range wide enough to convert frequency variations to amplitrude variations. There would be no well defined phase for the Coh2 algorithm to use. | ||

| ||
|
Figure 16. The phase noise of VCO.
At close range where the noise is high it can be analyzed with the Perseus directly. Figure 17 shows the Linrad screen in AM Coh2 mode. The audio output was recorded and when analyzing it as a two channel signal the screen looks like figure 18. | ||

| ||
|
Figure 17. VCO directly to the Perseus (through an attenuator).
| ||

| ||
|
Figure 18. The .wav from VCO that was recorded as shown
in figur 17.
At 10 kHz the FM noise is 8 dB above the AM noise.
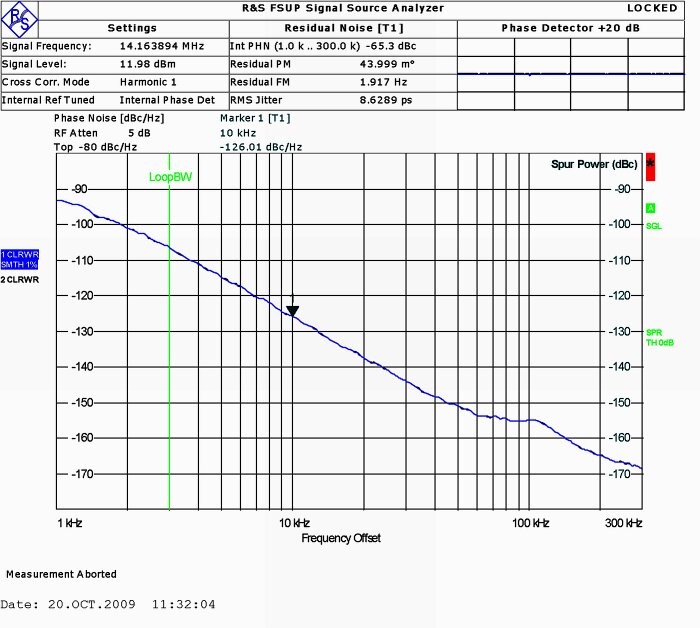
The free-running VCO is dominated by phase noise at close range. At 10 kHz frequency separation the the AM noise is 8 dB below the phase noise in figure 18, but the noise of the Perseus itself gives a significant contribution so the AM noise of the oscillator itself is probably a little lower than -150 dBc/Hz. FMThis oscillator has high phase noise and low AM noise. The reason is a common design error. The capacitance diode gets it control voltage through a large resistor. Otherwise the design is the same as VCO.At 10 kHz the phase noise is -126 dBc/Hz. See figure 19. | ||
| ||
|
Figure 19. The phase noise of FM.
The strong sideband noise is high above the noise floor in Perseus. See figure 20. | ||

| ||
|
Figure 20. FM directly to the Perseus (through an attenuator.)
| ||

| ||
|
Figure 21. The .wav from FM that was recorded as shown
in figure 20.
At 10 kHz the FM noise is 20 dB above the AM noise.
The AM noise is 20 dB below the phase noise in figure 21 that would be -146 dBc/Hz but the true level could well be lower. AMThis oscillator has high AM noise. It is a crystal oscillator followed by a buffer amplifier that gets its supply voltage directly from a 7012 without appropriate LF decoupling.The phase noise is at -155.6 dBc/Hz according to the FSUP as can be seen in figure 22. | ||

| ||
|
Figure 22. The phase noise of AM.
When this oscillator is connected directly to the Perseus one can clearly see a much higher sideband noise level. See figure 23. | ||

| ||
|
Figure 23. AM directly to the Perseus (through an attenuator.)
| ||

| ||
|
Figure 24. The .wav from AM that was recorded as shown
in figure 23.
At 10 kHz the FM noise is 14 dB below the AM noise.
In figure 24 the FM noise is 14 dB below the AM noise at 10 kHz. The FM noise in figure 24 is however dominated by the FM noise of the Perseus itself so the AM noise is higher than -141 dBc/Hz. Direct measurements of composite noise.Direct measurements with the Perseus at 10 kHz kHz frequency separation with 1 kHz bandwidth gives the results shown in the table below where also the phase noise measurements with the FSUP are listed. Sideband noise at 10 kHz
Unit Composite Phase
(dbc/Hz) (dBc/Hz)
OLDREF -148.4 -173
VCO -141.8 -142.6
FM -125.9 -126.0
AM -138.1 -155.6
The oscillator under test was connected through an attenuator
to the Perseus input. The Perseus was set for Preamp OFF,
dither OFF, Presel OFF and no attenuation.
The signal level was adjusted to 1 dB below saturation.
The composite noise was obtained as the difference of the
S-meter readings on the signal and 10 kHz below.
The noise floor of the Perseus itself is obviously -148.4 dB and that is low enough to allow direct measurement of the sideband noise of the LC oscillators. It is interesting to note that the simple free-running VCO is quite good. NEWREFThis oscillator is about 6 dB better than OLDREF. At a power level of +14 dBm it did not produce a realistic result on the FSUP.I have modified slightly for a power level of 16.1 dBm. I think -179.5 dBc/Hz is a bit below what can be measured on an FSUP. After all the FSUP is a wideband instrument.... To SM 5 BSZ Main Page |