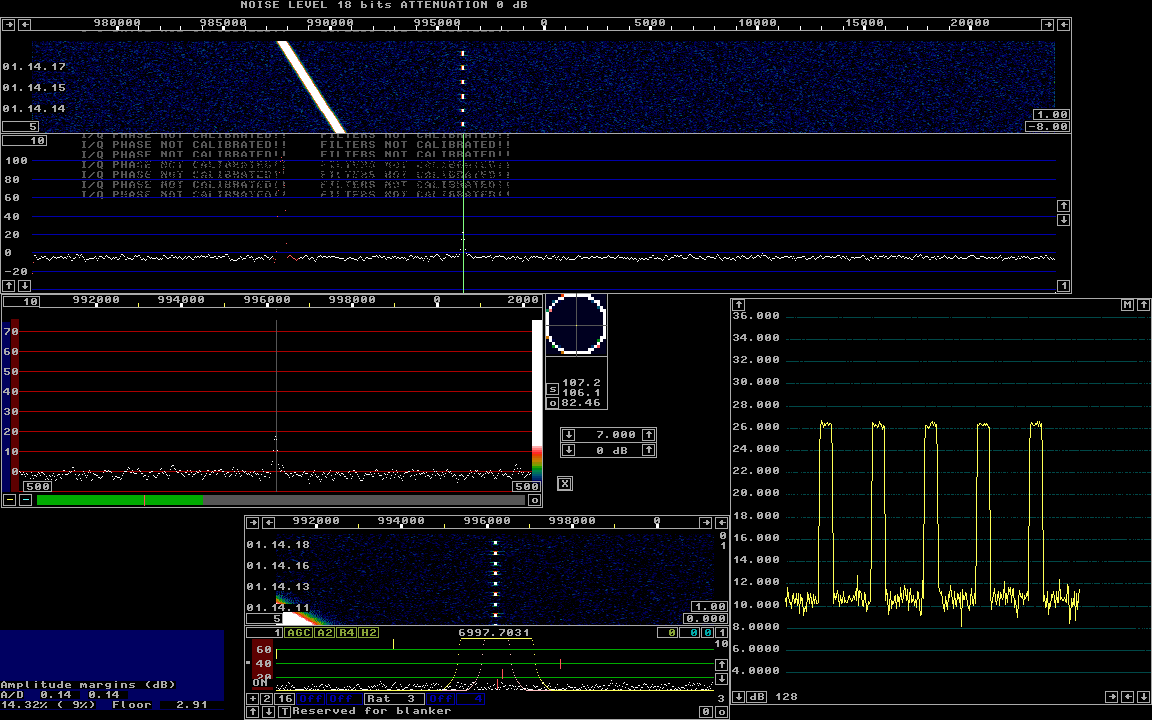
General.In order to get the lowest possible system noise temperature at the input of the MAP65 decoder it is not only necessary to make sure that the noise floor from the antenna mounted preamplifier is well above the noise floor of subsequent analog amplifier stages. The noise floor must also be well above the quantization noise of the A/D converter and it must also be well above the quantization noise in the USB channel in e.g. SDR-IQ that uses only 16 bit data for the USB transfer even though 24 bit data is available from the A/D converter after resampling.MAP65 and 16 bit data.When the MMX implementation of the first backward FFT routine is selected in Linrad, First backward FFT version = 1 in the mode setup menu, there are two more places where the noise floor must be well above the quantization noise.The first FFT always produces transforms in floating point format. They are converted to 16 bit integers to fit the 16 bit backwards FFT. This conversion produces rounding errors that add random noise as well as non-random errors in case strong signals are present. It is essential that the noise floor is well above the quantization noise, another term for noise due to rounding errors. The rounding error can be in the range -0.5 to +0.5 bit and its RMS amplitude is about 0.3 bit. Consequently the output from the first FFT has to be at least 3 bits RMS for those frequency bins that contain noise only. Otherwise the quantization noise would contribute more than 1% to the total noise. The backwards transform itself can provide more or less gain. It is also essential that the noise floor at the output, the 16 bit TIMF2 data stream, is well above the quantization noise. Noise is of course added in each butterfly loop of the FFT algorithm, but if the contribution is less than 1 % at the input as well as on the output, the total degradation is acceptable. The user can attenuate the 16 bit TIMF2 data before sending it to MAP65. It is of course also important to keep the signal level high enough to avoid quantization noise in the attenuation process. The level of the noise floor in the signal actually sent to MAP65 must be well above the quantization noise of the attenuated signal which means that the noise floor sent to MAP65 should be at least 3 bit RMS. The images on this page show screen dumps that demonstrate how the S/N is degraded in case inappropriate level parameters are selected. The internal generator.The internal generator in Linrad has been changed so it can be enabled regardless of what signal source Linrad is set up for. (In previous versions it could only be enabled when files from the hard disk were processed.) Use F1 on the main menu occasionally. That will give a list of all the keyboard commands. The internal generator is F11.The noise floor and the level of the strong signal can be set from the keyboard but frequencies and the level of the weak signal have to be set inside the routine itself which is located within the module rxin.c. Ideal performance.Figure 1 shows the Linrad screen when floating point is selected for the backwards FFT1. The resulting TIMF2 time function is analyzed by the second FFT of Linrad itself. It is exactly the same time function that would be sent to MAP65 in float format over the network (assuming no programming errors). Future MAP65 versions may be able to receive float format, but current versions are restricted to 16 bit integers only.Linrad is set to receive 24 bit data at 48 kHz from a soundcard. The internal generator is set to produce a noise floor with a RMS power of 18 bits with a strong signal very close to saturation. The relevant processing parameters for figure 1 are like this: First FFT bandwidth (Hz) = 100 (bw is 117Hz) First FFT window (power of sin) = 8 (Gaussian) First FFT amplitude = 100 First backward FFT version = 0 (float format) First backward FFT att. N = 2 (min attenuation) Second FFT bandwidth factor in powers of 2 = 0 Second FFT window (power of sin) = 4 Second forward FFT version = 0 (float arithmetics) |
 |
|
Fig 1. The internal test signal of Linrad with floating
point arithmetics.
There is no quantization noise internally in Linrad and the
S/N is about 15.7 dB in the S-meter graph.
Figure 1 is made after the A key is pressed so amplitude margins are shown in the lower left corner of the screen. The signal level is 0.14 dB from saturation. That corresponds to 0 dB attenuation of the strong signal as indicated in the top line. The strong signal can be attenuated in 20 dB steps with the F8 key. The strong signal sweeps downwards at a fixed rate. It is red in the main spectrum which means that the time function computed from it will be routed outside the noise blanker. Whether the weak signal is visible or not in the spectrum graphs on this page depends on the exact time when the image was captured. It is not relevant, the true characteristics of the weak signal (including artifacts) is well visible in the S-meter graphs. Rounding errors at the First FFT output.Figure 2 shows the screen with all parameters the same except the one controlling the arithmetics:First backward FFT version = 1 (int 16 format) Note that the first backwards FFT runs at maximum gain so there is negligible quantization noise on the output. |
 |
|
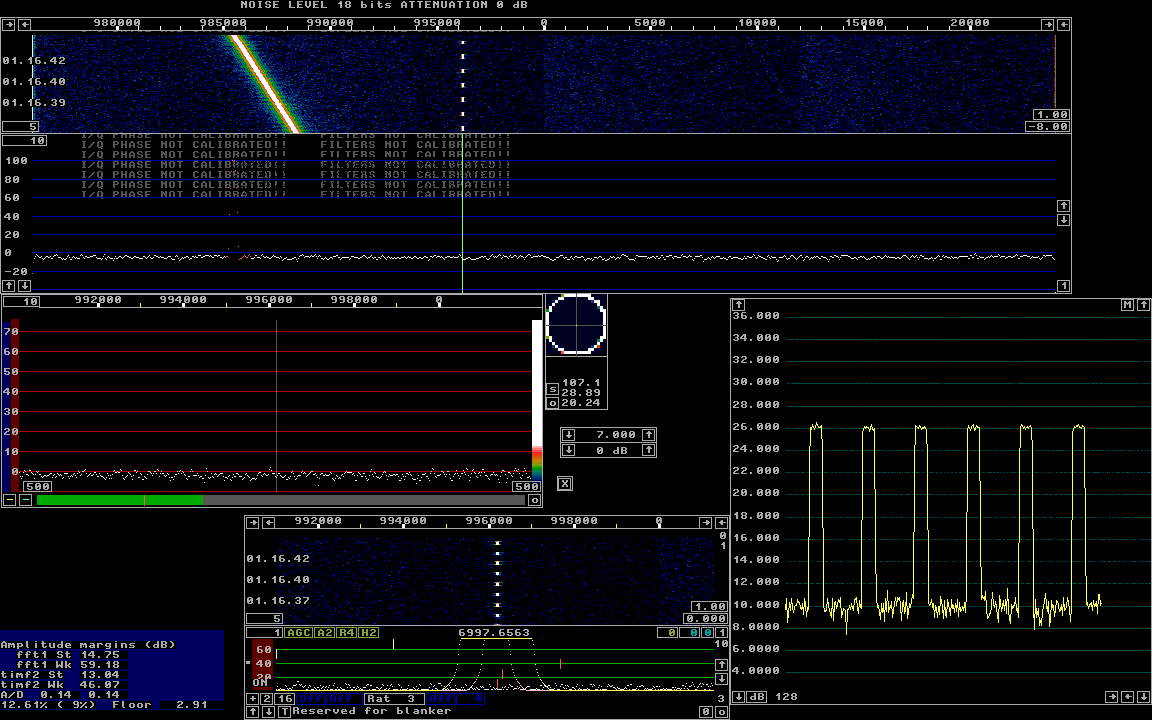
Fig 2. The internal test signal of Linrad with 16 bit
arithmetics.
Parameters are identical to those in figure 1 except for the one
controlling the output format of FFT1.
Note that S/N in the S-meter graph is higher than in figure 2
that is an artifact. See text.
A comparison of figure 1 and figure 2 might suggest that the settings in figure 2 would be advantageous since S/N is a little better in figure 2. That is an artifact however the better S/N is present only for strong signals. Those signals that are well above the noise in the FFT1 bandwidth of 117 Hz. The noise in each FFT bin is too low to be represented by the bit size of the 16 bit format which means that noise as well as real signals of comparable level to the noise in 117 Hz bandwidth is suppressed. Most of the FFT bins on the noise floor are zero and MAP65 performance would be very poor. The noise visible in the waterfall is not the antenna noise but quantization noise. Signals at the noise floor would be absent since the rounding not only adds noise. It attenuates real signals also if they are below the noise floor in the bin bandwidth of the first FFT. To understand the degradation displayed in figure 2, compare it to figure 3 which has 12 dB less quantization noise. Figure 3 shows an equivalent screen to figures 1 and 2. Here the amplitude at the first FFT output is 4 times larger while the gain of the first backwards FFT is 4 times lower. That means that the negligible quantization noise in the output is identical in figures 2 and 3. The parameters are: First FFT bandwidth (Hz) = 100 (bw is 117Hz) First FFT window (power of sin) = 8 (Gaussian) First FFT amplitude = 400 First backward FFT version = 1 (integer format) First backward FFT att. N = 4 Second FFT bandwidth factor in powers of 2 = 0 Second FFT window (power of sin) = 4 Second forward FFT version = 0 (float arithmetics) Only two parameters differ from those of figure 2. |
 |
|
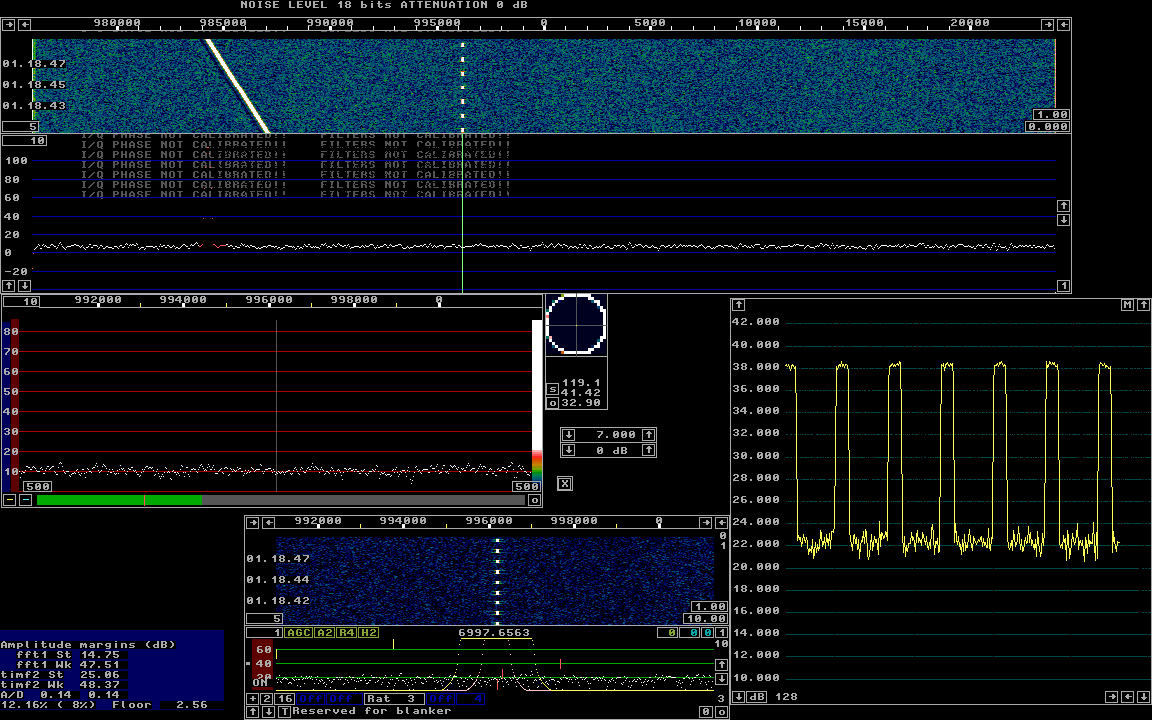
Fig 3. The internal test signal of Linrad with 16 bit
arithmetics.
Here the amplitude into the first FFT is 4 times (=12 dB)
higher than in figure 2 while the gain of the first backwards
FFT is 4 times lower (=12 dB).
Figure 3 shows a situation where quantization noise is contributing but where the degradation is modest. Compare to figure 2 where the noise floor makes a jump at the center frequency in the main waterfall which is computed from the timf2 signal. In figure 2 rounding errors also produce sideband noise on the strong signal. In figure 3 there is a small black band close to the strong signal. Frequencies near the strong signal are attenuated by the selective AGC and therefore the noise floor is suppressed. Not much however. Operating Linrad like that could perhaps be motivated under severe interference conditions with extremely strong local stations and difficult pulse interference from static rain. |
 |
|
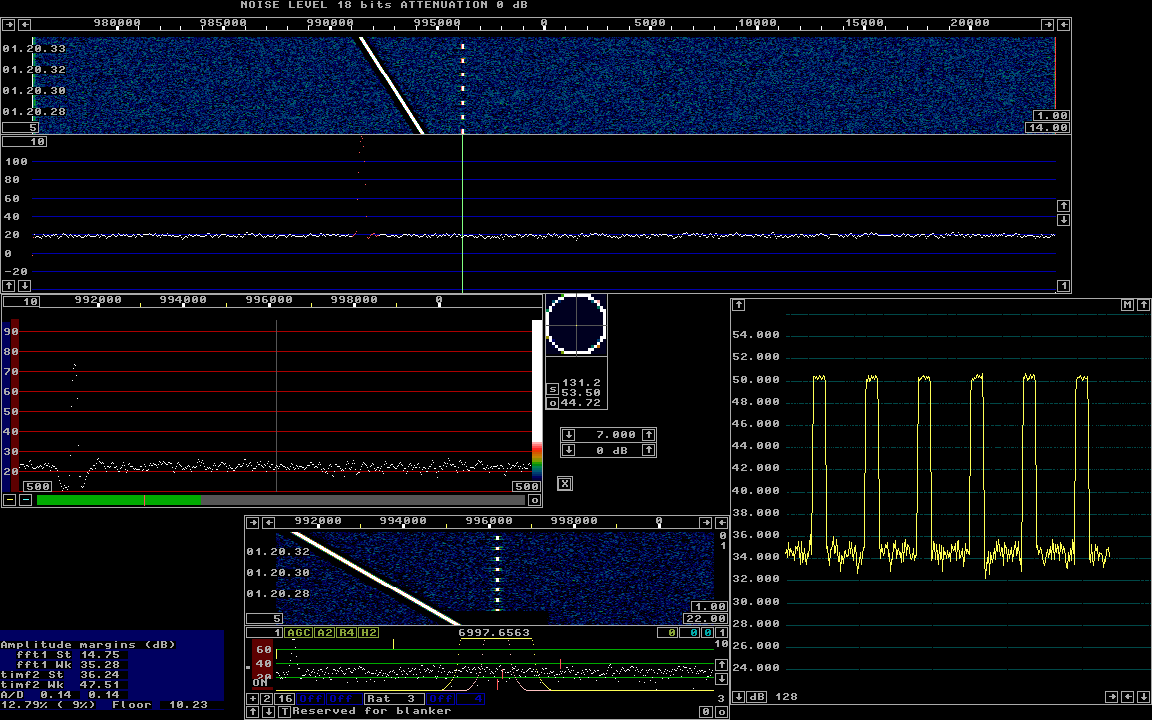
Fig 4.The internal test signal of Linrad with 16 bit
arithmetics.
Here the amplitude into the first FFT is 16 times (=24 dB)
higher than in figure 2 while the gain of the first backwards
FFT is 16 times lower.
Figure 4 shows a normal situation for Linrad while using 16 bit arithmetics. The parameters are like this: First FFT bandwidth (Hz) = 100 (bw is 117Hz) First FFT window (power of sin) = 8 (Gaussian) First FFT amplitude = 1600 First backward FFT version = 1 (integer format) First backward FFT att. N = 6 Second FFT bandwidth factor in powers of 2 = 0 Second FFT window (power of sin) = 4 Second forward FFT version = 0 (float arithmetics) These parameters provide 16 times more gain (24 dB) compared to figure 1. The output from the first FFT has a noise floor well above 1 bit so there is negligible quantization noise. The gain of the first backwards FFT is 16 times smaller so the circumstances at the output of the backwards FFT are identical in figures 2, 3 and 4. A comparison of figures 2, 3 and 4 shows that S/N for a relatively strong signal is similar. A comparison of fig 4 and fig 2 shows an interesting difference in the noise floor. In figure 4 the noise floor near the strong sweeping signal is about 10 dB below the general noise floor. This shows that the quantization noise is at least 10 dB below the noise floor of the antenna signal. The high resolution spectrum and the waterfall display the same signal. In figure 4 the 10 dB lower level is visible in the high resolution spectrum. The waterfall is black. In figure 2 the waterfall shows a colour indicating a level well above the wideband noise floor. That is quantization noise. The important information to MAP65 users is that the First FFT gain has to be set high enough for the antenna noise floor to well overcome the quantization noise at the FFT1 output in case 16 bit arithmetics is used. The number after Floor in the lower left corner of the screen should be in the order of 10 which corresponds to having the noise floor 10 times above one bit (=20 dB) in the 16 bit format. Placing the noise floor below 20 dB in the main spectrum is a bad idea when 16 bit arithmetics is used. In the float format there is no need to decrease the gain of strong signals. They just have to be routed outside the noise blanker. That is why there is no black zone around the strong signal in figure 1. To SM 5 BSZ Main Page |