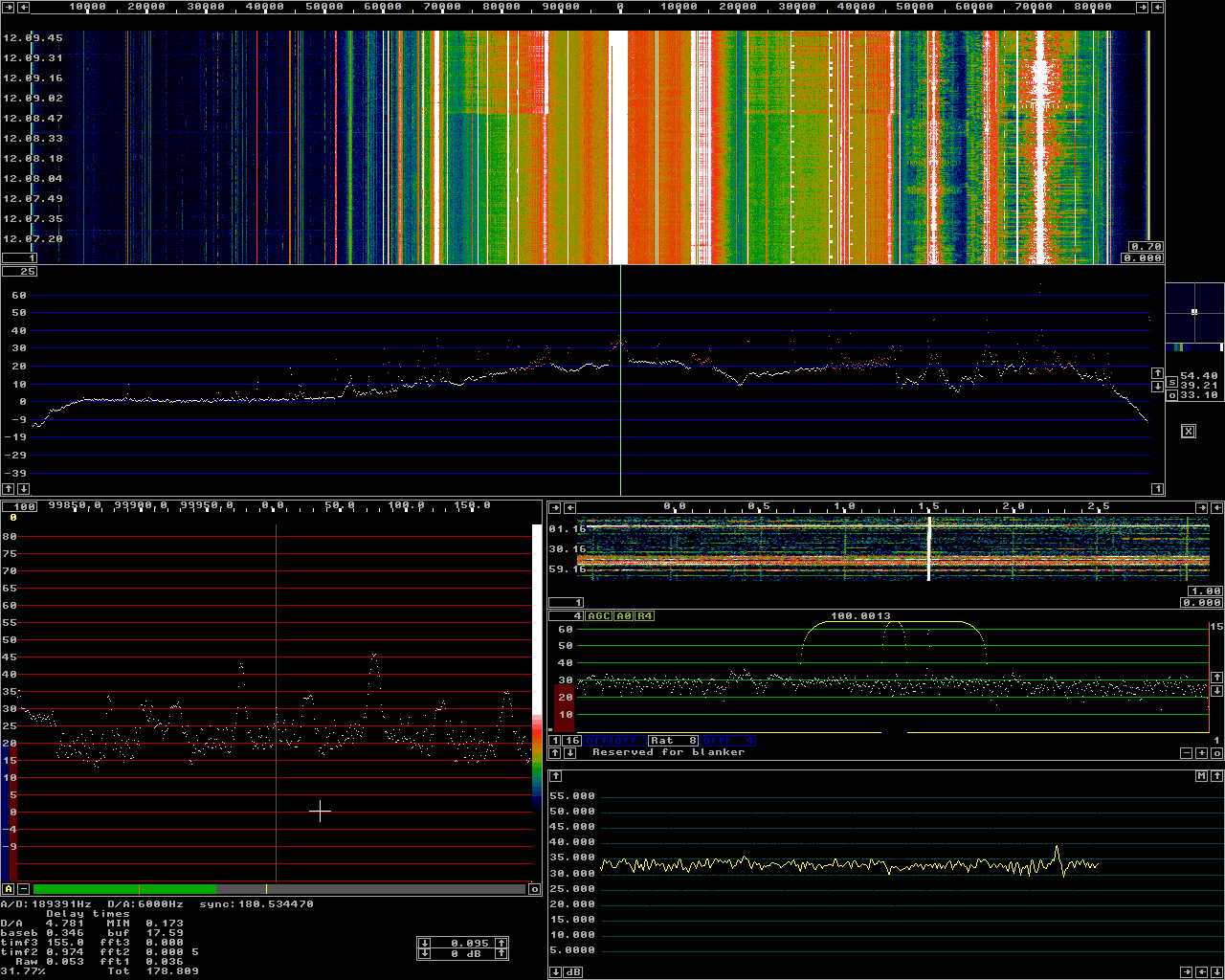
Fig 1.Loran-C in the baseband window. See text.
GeneralLinrad can be used to produce waterfall graphs at very narrow bandwidths while interference fighting with the noise blanker is done at a high bandwidth. In case floating point routines are selected for the seconf FFT, the maximum size is 65536 but when the MMX routines are selected the limitations are given by the hardware. The time it takes to compute a transform of the second FFT must not be larger than the time allocated for timf1, the buffer into which the hardware device driver stores its data. On a pentium IV this limit is an fft size of 8388608 (Linrad-02-20). Another limit is that the total time spanned by the second FFT must not exceed 200 seconds. The baseband has to be run at a 21 to 210 lower sampling rate than the hardware supplies to Linrad and the maximum bandwidth in the baseband is half the baseband sampling rate or the largest bandwidth that the selected D/A output speed will allow.The examples given below are not selected because they are particularly interesting. They are just intended to give an idea about what can be done. Linrad versions in the 2.xx series below 2.20 have limitations at much smaller transform sizes due to changes made in the transition from the single threaded 1.xx series to a multi-threaded structure. The Loran-C signal at 100 kHz.Figure 1 shows the spectrum with an SDR-14 set at 95 kHz to receive from 0 to 183kHz. The main spectrum, the first FFT is computed with an fft size of 16384. The main waterfall, the second FFT, is computed with an FFT size of 262144 for a bin separation of 0.72 Hz. The Loran-C carrier is weak, it is not too easy to find in the hires graph where the second fft is plotted with one pixel per bin.The baseband graph and waterfall are computed from 32768 transforms that are applied to a signal that is downsampled by a factor 210 (=1024 times) The sampling speed is thus 184.95 Hz for the baseband and the bin separation is 5.6 mHz (milli Hertz.) The Loran-C carrier is strong at such narrow bandwidth. There is no visible path modulation, the resolution should be 10 mHz since a sine squared window is used for the baseband and that is in fair agreement with what can be seen in figure 1. It is obvious that the SDR-14 is off by 1.5 Hz, a frequency error of 15 ppm. |

Fig 1.Loran-C in the baseband window. See text. |
The spectrum of JT65Linrad allows very large fourier transforms when the second FFT is enabled and when the mmx routines are selected. Figure 2 shows the spectrum of the audio output from another computer running the wsjt program transmitting an ordinary JT65 message. |
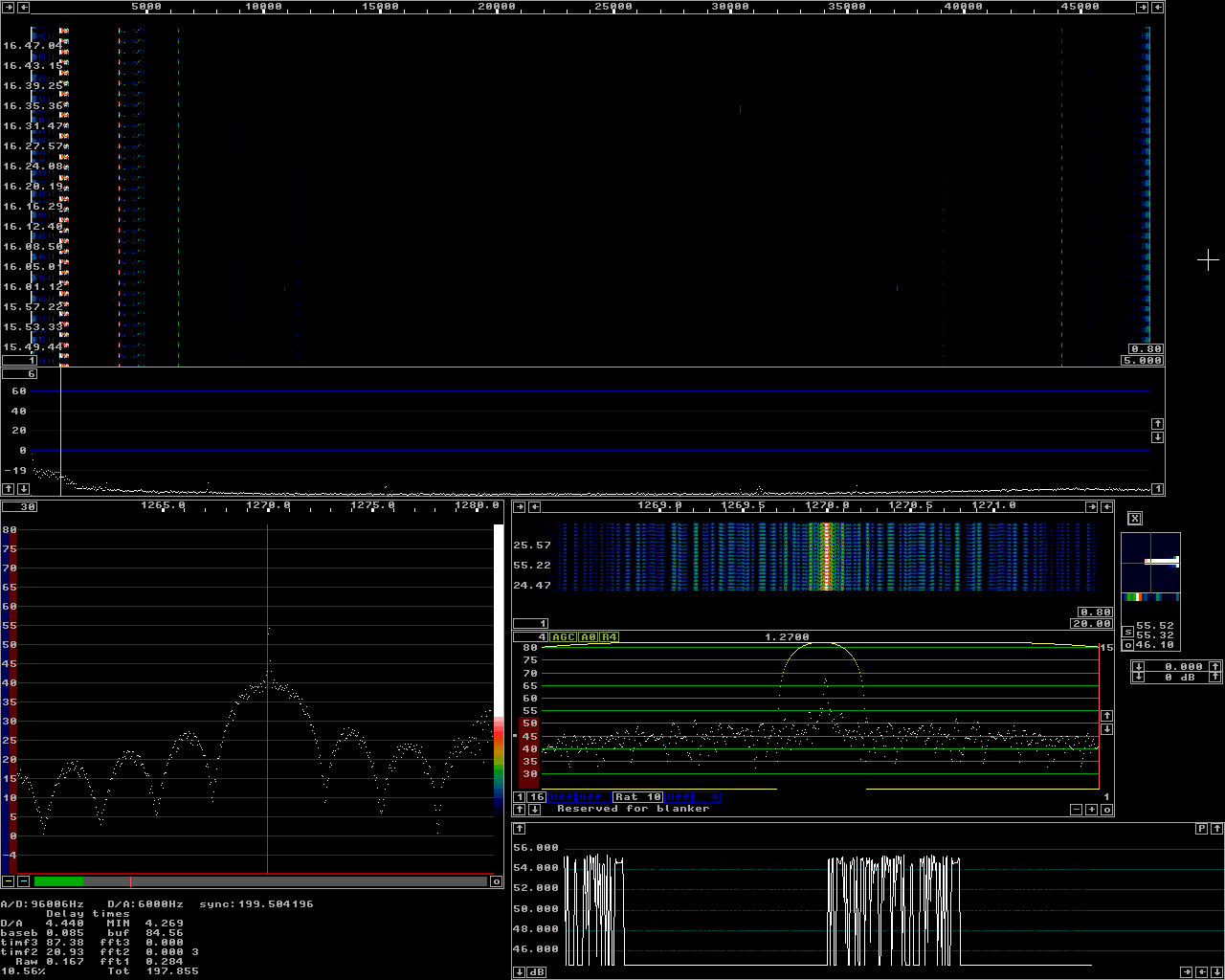
Fig 2.A JT65 signal with the sync tone at 1270 Hz. The sampling speed is 96 kHz. |
|
The only purpose of the high sampling speed,
96 kHz in figure 2 is to show that the second FFT
can be run with a transform size of 1048576 for a
bandwidth of about 0.09Hz with a sine squared window.
In this particular case it would have been more sensible
to sample at 6 kHz and produce an identical result
with a 131072 transform.
The first mixer bandwidth reduction is set to 256
(parameter value=8) and the baseband transform size is set to
32768 (15 in the upper right corner of the baseband graph.)
Since FFT2 runs at 48 kHz for a complex transform,
(real input at 96 kHz)
the baseband runs at 187.5 Hz for a bin width of 5.7 mHz (milliHz)
and a resolution in the baseband of 11.4 mHz.
The baseband transform spans a time of 175 seconds and therefore a single transform contains more than one period of the wsjt transmission. The sync tone phase is not stable between separate transmissions and therefore the carrier for the sync tone is widened. (The sync tone can be seen as an AM modulated signal) Each line in the waterfall spectrum is produced from a single transform. Since the transforms overlap by 50% each line corresponds to 87.5 seconds in the baseband. The baseband waterfall shows about 1.5 hours while the main waterfall shows about one hour. To SM 5 BSZ Main Page |