A CW receiver with a small time delay and a fast waterfall graph.

A CW receiver with a small time delay and a fast waterfall graph.
(May 28 2006)

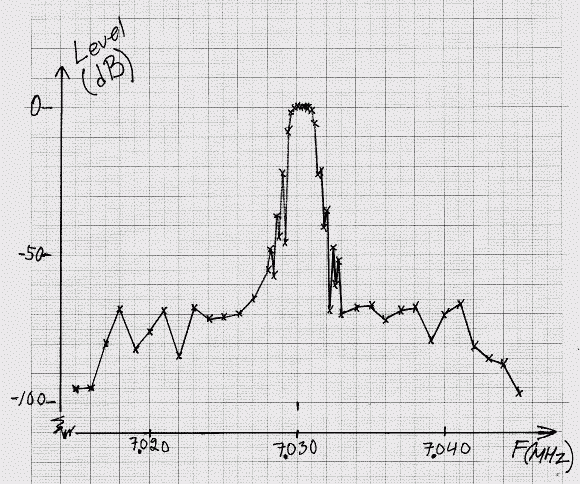
Linrad uses two or three filters after each other and the total time delay is the sum of the individual delays. In this example the second FFT is deselected and the bandwidth of the first FFT is set to 800 Hz with a sine squared window. This means that the FFT1 transforms spans a time of about 2/800 seconds (2.5 ms). Actually the FFT size becomes 256 at a sampling speed of 96 kHz so the delay caused by fft1 is 2.666 ms because all 256 data points have to be collected before computation can begin.

In this example the first mixer downsamples by a factor of four for a sampling speed of 24 kHz and with a 64 point FFT for the baseband the time spanned also becomes 2.666 ms. Since the baseband FFT can be processed immediately after one block of data has been delivered from fft1 the delay times do not have to add. In addition to the unavoidable delay from the filters there is also delay caused by the input and output block size. Linrad estimates the processing delay from the FFT sizes and sets very small buffers in case the user has selected small transforms.

The parameters affecting processing delay in par_wcw are the following:
First FFT bandwidth (Hz) [800]
First FFT window (power of sin) [2]
Enable second FFT [0]
Enable AFC/SPUR/DECODE [0]
First mixer bandwidth reduction in powers of 2 [2]
Output delay margin (ms) [8] (This parameter must be set differently on different systems)
Output sampling speed (Hz) [48000]
A/D speed [96000]

The entire set of parameters (for Linrad-02.14) can be downloaded here ldfwpar.tbz (for Linux) or here ldfwpar.zip (for Windows) These parameters are for "A=Weak signal CW" but can equally well be applied to the other modes.

The baseband FFT always uses a sin squared window and it is obvious that it can not produce any really good filter with a bin separation of 375 Hz. Figure 1 shows the filter characteristics as measured with a frequency stepped signal generator while Linrad is set at a fixed frequency of 7.030 MHz.

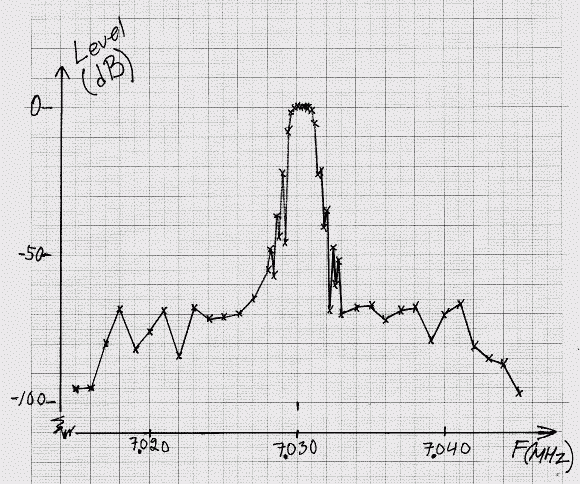
Fig 1. Frequency response of Linrad with the parameters of this page.

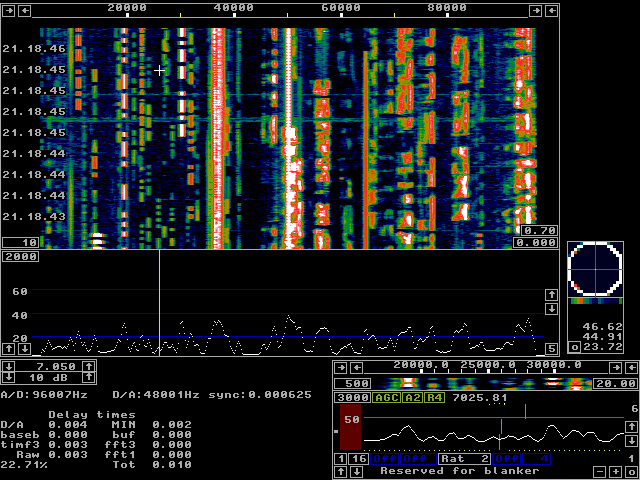
The time delay varies depending on the operating system and possibly on the sound system. Figure 2 shows the screen when running linrad in terminal mode with svgalib and ALSA under Debian Etch on a Pentium 4 at 2.667 GHz.

Direct to results for MS Windows

The parameters used on this page are extreme and put high requirements on latency of the operating system as well as on the efficiency of the graphics. Debian Etch with kernel 2.6.15-1-486 runs well both with svgalib and with X11. Figures 3 and 4 show the performance with 24 bit colours and 8 bit colours respectively.

Fig 2. Debian Etch with ALSA and svgalib on a PentiumIV at 2.667 MHz. The time delay through Linrad from antenna to loudspeaker is 10 milliseconds.

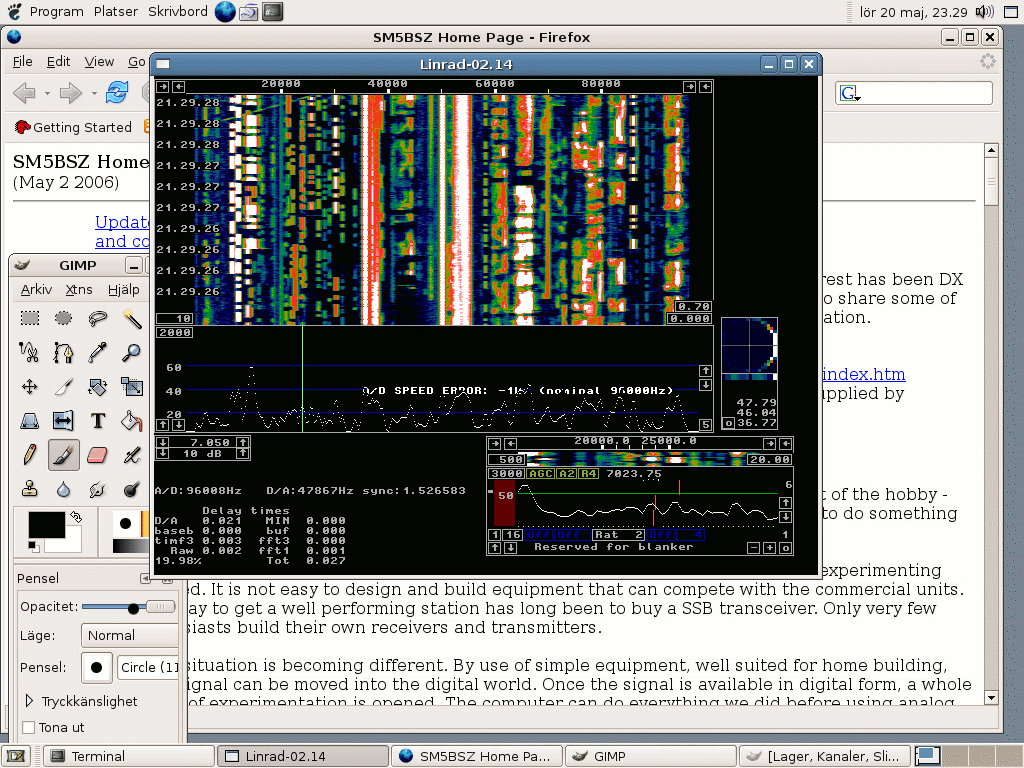
Fig 3.Debian Etch with ALSA and X11 with a colour depth of 24 bits on a PentiumIV at 2.667 MHz. The time delay through Linrad from antenna to loudspeaker is 27 milliseconds, but this is not quite enough time to allow for the slow response of the X11 server at a colour depth of 24 bits. As can be seen in the figure there is no margin at all.

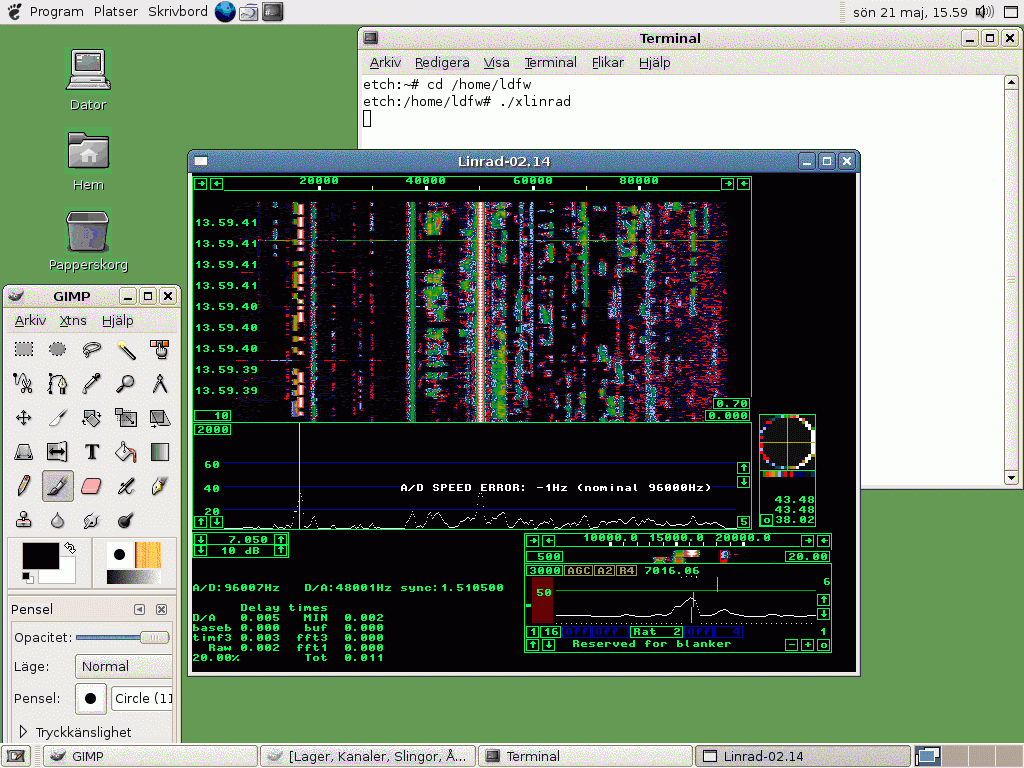
Fig 4.Debian Etch with ALSA and X11 with a colour depth of 8 bits on a PentiumIV at 2.667 MHz. The time delay through Linrad from antenna to loudspeaker is 11 milliseconds. At a colour depth of 8 bits the X11 server is fast enough. Note that the colours are correct on the screen while Linrad is running. This image is captured with Gimp and Gimp uses its own palette, not the one used while Linrad is running.

Red Hat 9 with kernel 2.4.20-8 has more latency as compared to Debian Etch. The delay through Linrad is typically the same, about 10 ms, but under Red Hat 9 the delay occasionally becomes larger and it is necessary to set a larger margin for the delay through Linrad. Figures 5 through 7 show the behaviour of Linrad under Red Hat 9 with svgalib and X11.

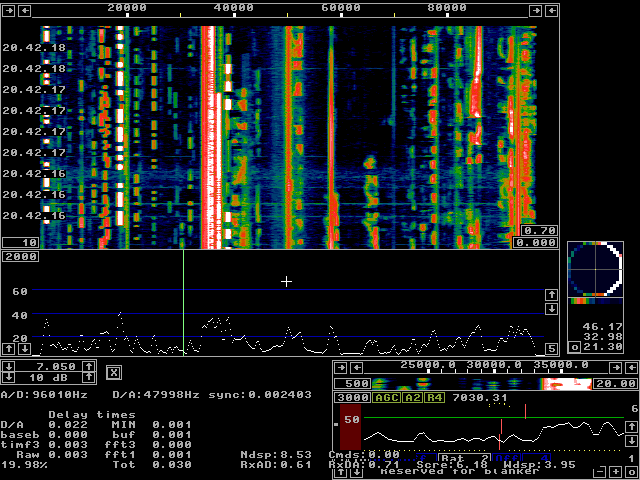
Fig 5. Red Hat 9 with OSS and svgalib on a PentiumIV at 2.667 MHz. The time delay through Linrad from antenna to loudspeaker is 30 milliseconds. At the moment when this screen was captured the margin was 22 ms, but occasionally the margin becomes close to zero.

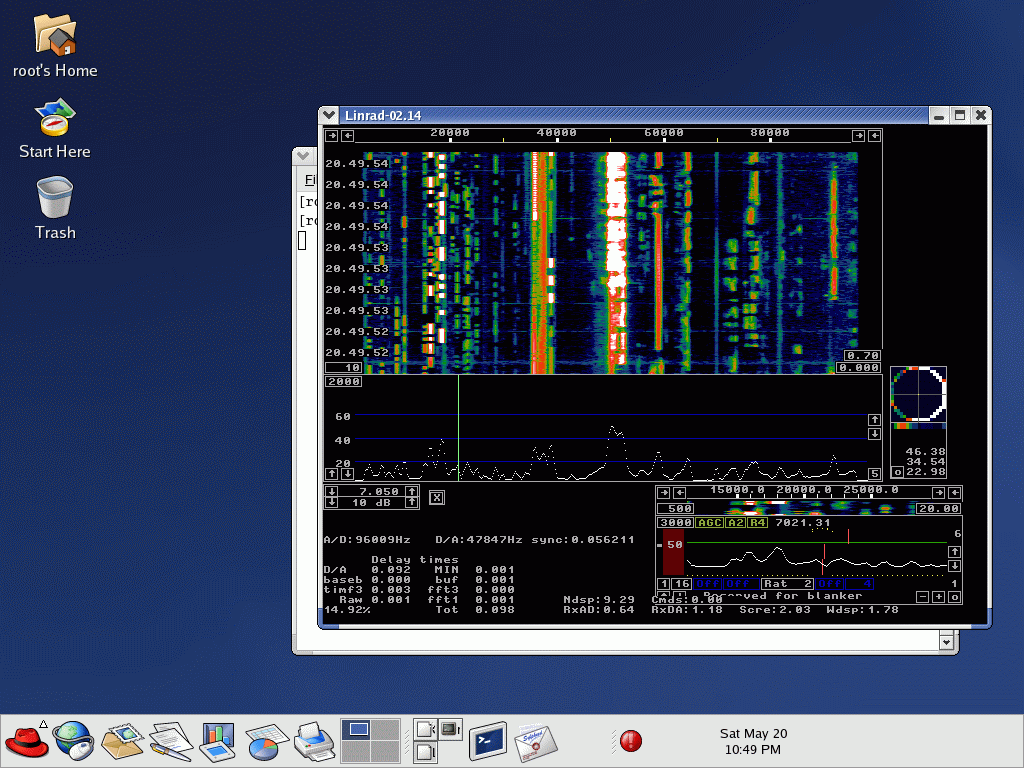
Fig 6. Red Hat 9 with OSS and and X11 with a colour depth of 24 bits on a PentiumIV at 2.667 MHz. The time delay through Linrad from antenna to loudspeaker is 98 milliseconds, but this is not quite enough time to allow for the slow response of the X11 server at a colour depth of 24 bits. As can be seen in the figure the margin is very small.

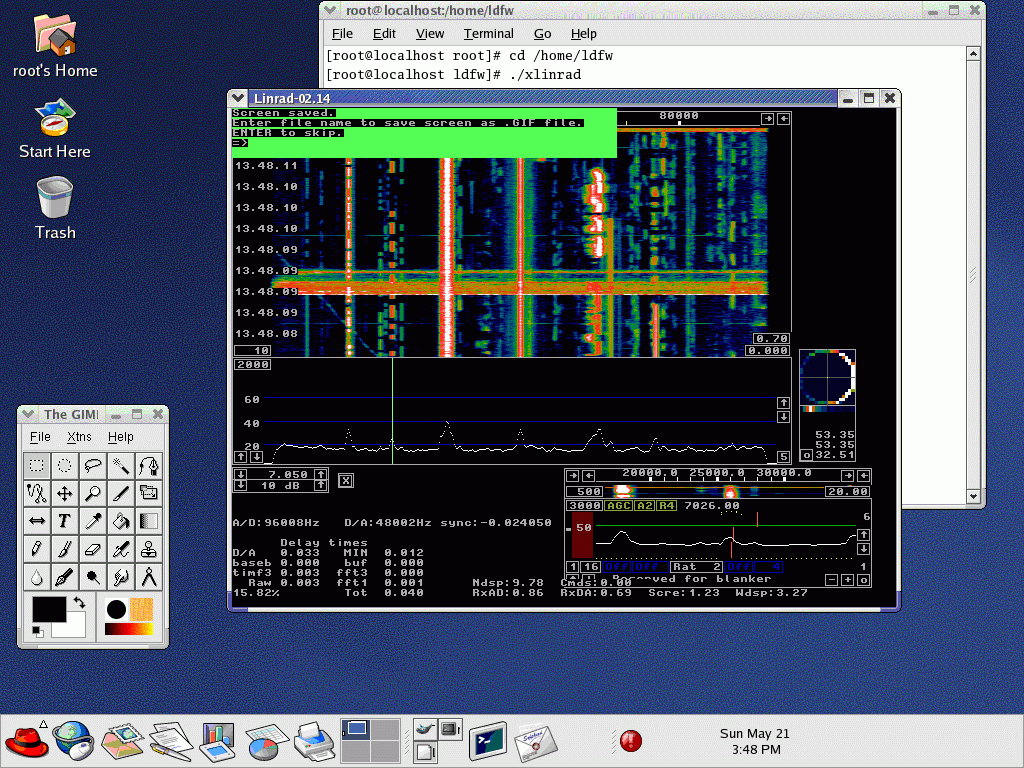
Fig 7. Red Hat 9 with OSS and and X11 with a colour depth of 8 bits on a PentiumIV at 2.667 MHz. The time delay through Linrad from antenna to loudspeaker is 40 milliseconds.

Windows 2000 runs well on the 2.7 GHz PentiumIV. The screen typically looks like fig 8. The output delay margin parameter is set to zero but the minimum margin is 29 ms. The latency of Windows 2000 is good and it should be possible to achieve a total delay of about 15 ms.

It is possible to run the demanding processing parameters of this page on a 650 MHz PentiumIII under Windows 2000. Figure 9 shows what the screen looks like. Also Windows 98 runs fine on the 650MHz PIII as can be seen in figure 10.

A PentiumII at 350 MHz is too slow for Microsoft Windows. Windows 98 gets a totally corrupted input with a spectrum that shows each signal at four locations on the frequency scale when the original drive routine was used. After the Delta 44 drive routine was uprgaded to the latest one, the spectrum looks a bit better with each signal occuring at two places. Figure 19 shows what the spectrum looks like with a test signal. By sweeping this test signal over the frequency range one can find that the sampling actually takes place at 48 kHz and that Windows 98 uses some simple algorithm to deliver twice the sampling frequency to Linrad. Only 50% of the frequency range contains valid data, what is outside is just an artifact from the up-sampling process.

Windows 2000 does not have any problem with the input, but the PentiumII CPU is not quite fast enough as can be seen in figure 11. To use Linrad on the PentiumII under Windows 2000 one has to select less extreme parameters and then the delay through Linrad becomes something like 100 milliseconds.

Fig 8. Windows 2000 on a PentiumIV at 2.667 MHz. The time delay through Linrad from antenna to loudspeaker is 42 milliseconds.

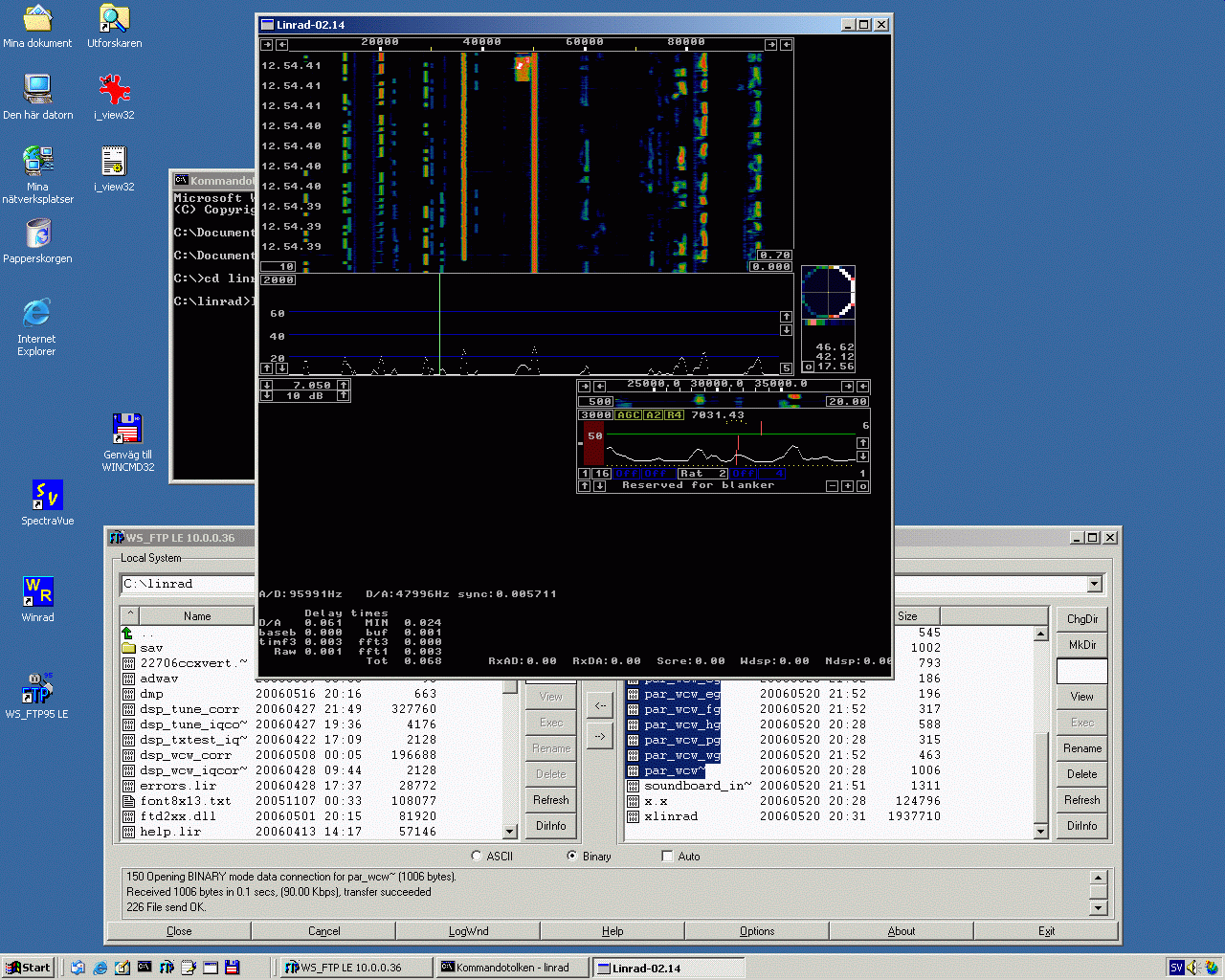
Fig 9. Windows 2000 on a PentiumIII at 650 MHz. The time delay through Linrad from antenna to loudspeaker is 68 milliseconds.

Fig 10. Windows 98 on a PentiumIII at 650 MHz. The time delay through Linrad from antenna to loudspeaker is 68 milliseconds.

Fig 11. Windows 2000 on a PentiumII at 350 MHz. This computer is too slow. About 20% of the data that should have been written to the output is missing. The speed of the data flow actually sent to the output is about 37 kHz. The soundcard runs at 48 kHz and the missing data is replaced by silence causing a steady carrier to sound as if it were keyed with about 80% duty at a keying speed of about 5 Hz.

When Linrad is run with svgalib in terminal mode under Linux the PentiumII at 350 MHz is very close to be fast enough as shown in figure 12. A PentiumIII is fast enough with a good margin as can be seen in figures 13 and 14. Mandrake 8.1 with a 2.4 kernel causes much less CPU load than Fedora 5 with a 2.6 kernel. The much lower latency in the modern kernel presumably has a cost in more overhead caused by more frequent task switching.

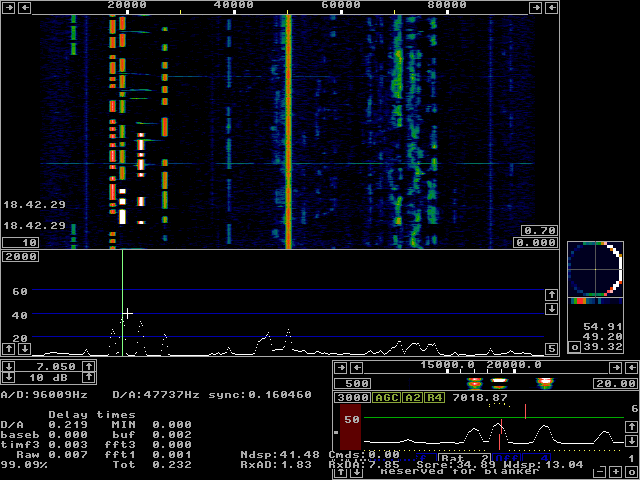
Fig 12. Mandrake 8.0 on a PentiumII at 350 MHz. The CPU load is close to 100% but the amount of missing data in the loudspeaker output is too small to be noticed by ear on normal signals.

Fig 13. Mandrake 8.1 on a PentiumIII at 650 MHz. The time delay is 24 milliseconds at a CPU load of 50%. This computer is fast enough to be used this way.

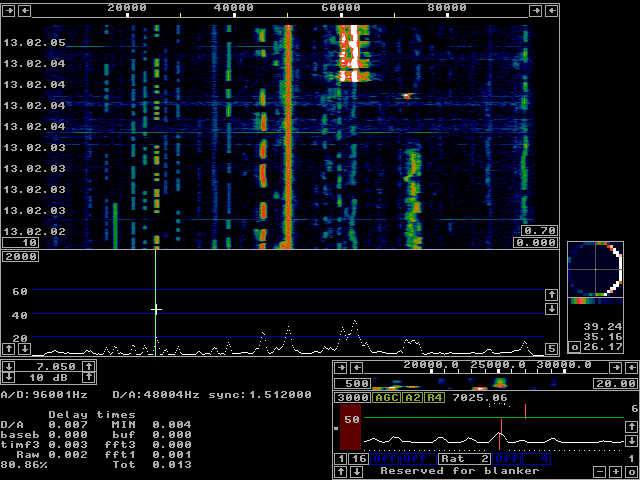
Fig 14. Fedora 5 on a PentiumIII at 650 MHz. The time delay is 13 milliseconds at a CPU load of 80%.

Under X11 Mandrake 8.1 does not work on the PentiumIII at 650 MHz despite the low CPU load. The latency is too long for parameters optimised for a modern Linux distribution regardless of whether a colour depth of 8 or 24 bits is choosen. See figures 15 and 16.

Under X11 Fedora 5 does not work at all on the 650MHz PentiumIII when a colour depth of 24 bit is selected as can be seen in figure 17. The colour depth is very important however. With a colour dept of 8 bit Fedora 5 runs fine on the 650 MHz PentiumIII as can be seen in figure 18.

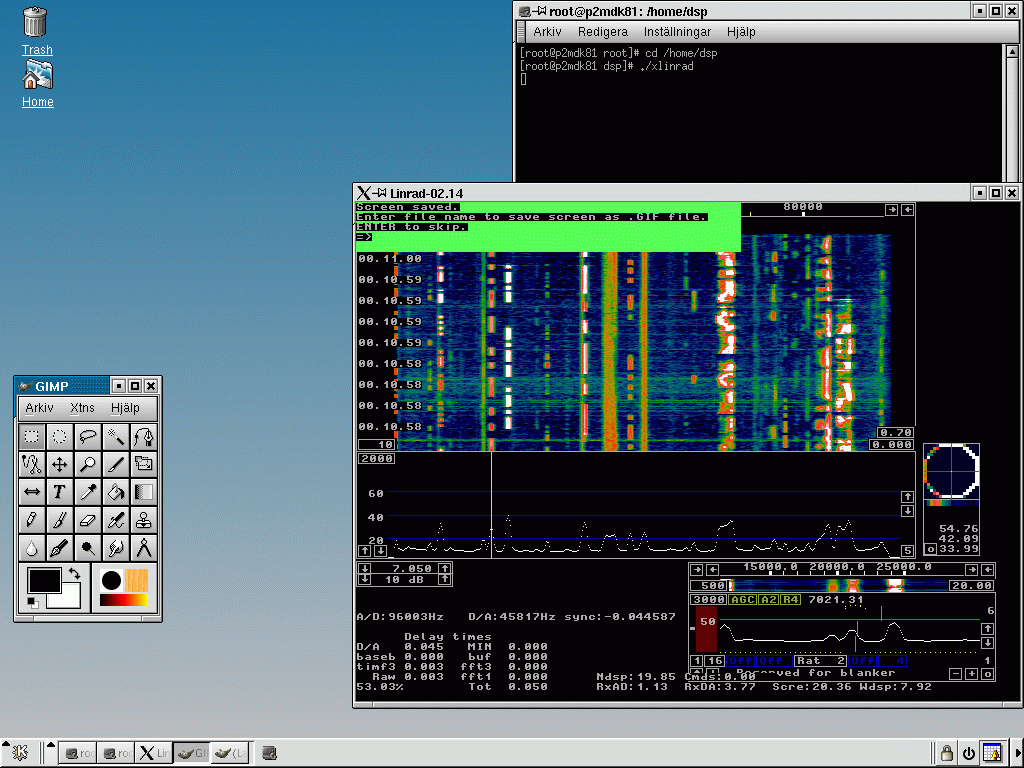
Fig 15. Mandrake 8.1 on a PentiumIII at 650 MHz with a colour depth of 24 bits. The latency of the X11 server does not allow the usage of very small buffers for the sound system. Note that the output speed is only 45 kHz, not 48kHz so part of the output is lost due to underrun errors.

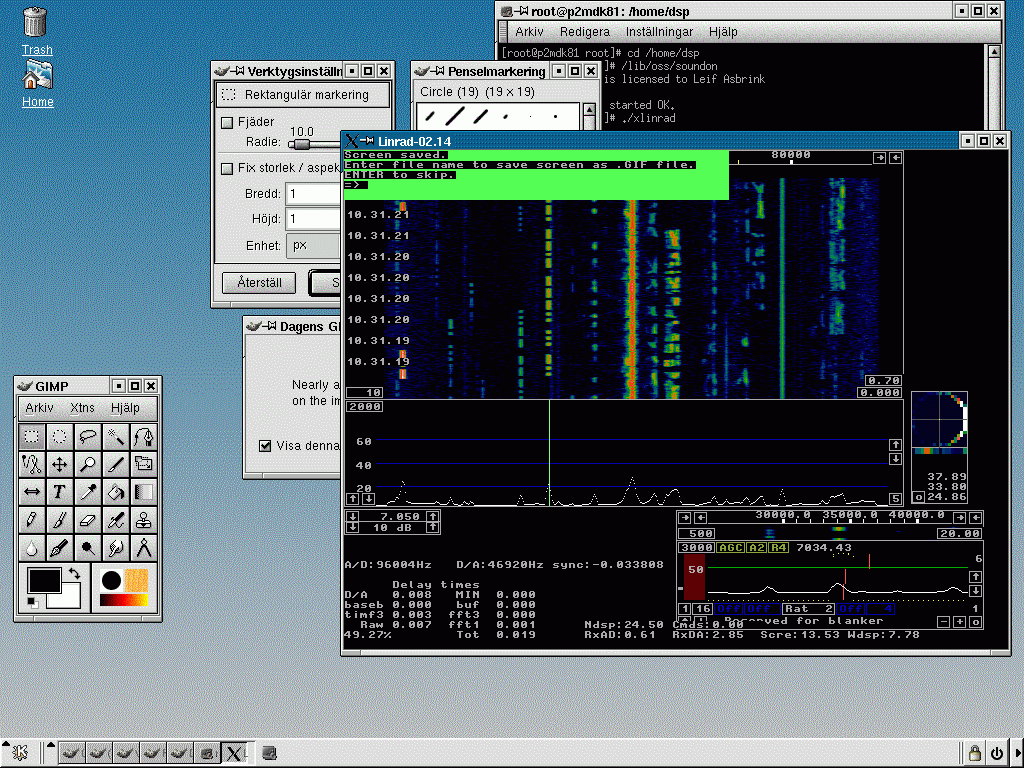
Fig 16. Mandrake 8.1 on a PentiumIII at 650 MHz with a colour depth of 8 bits. Very similar to figure 15.

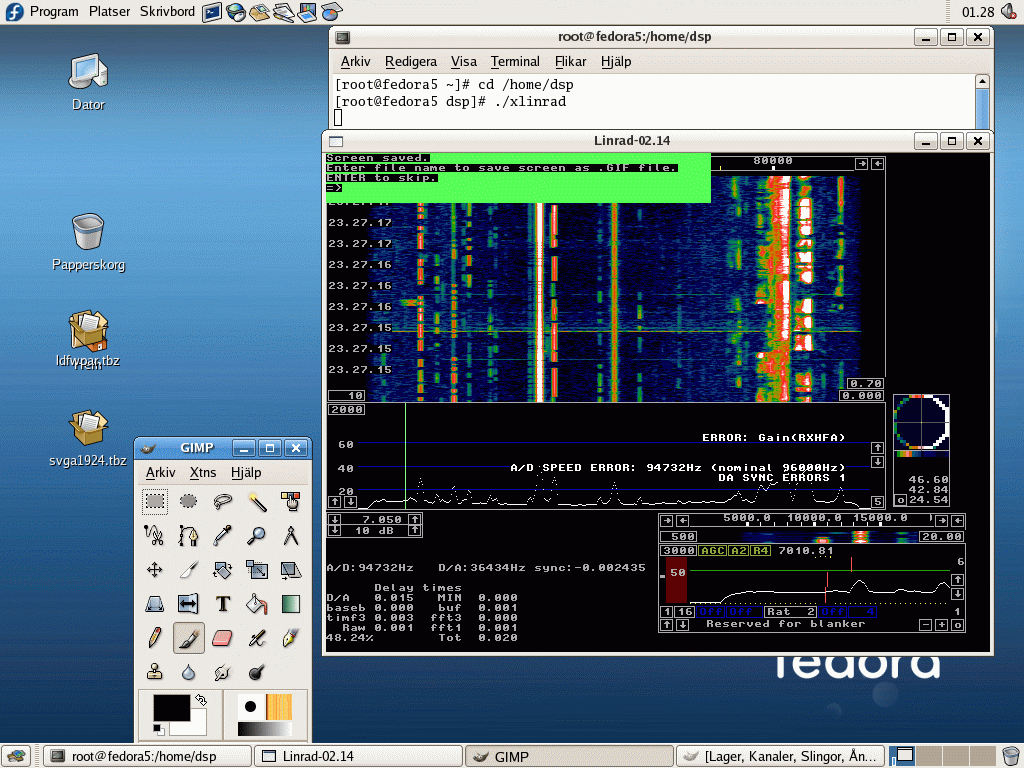
Fig 17. Fedora 5 on a PentiumIII at 650 MHz with a colour depth of 24 bits. The latency of the X11 server does not allow the usage of very small buffers for the sound system and data is lost both on the input and the output side.

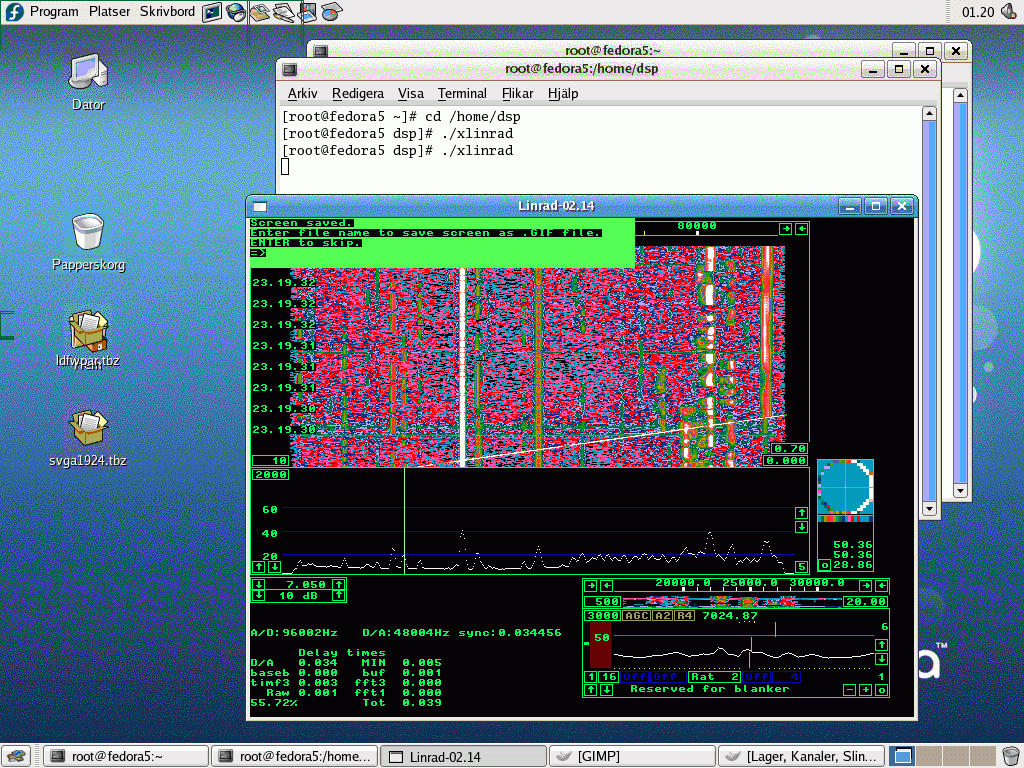
Fig 18. Fedora 5 on a PentiumIII at 650 MHz with a colour depth of 8 bits. This configuration works fine with a processing delay of 39 milliseconds. Changing colour depth makes a dramatic improvement under Fedora 5 contrary to Mandrake 8.1. Note that the colours are correct on the screen while Linrad is running. This image is captured with Gimp and Gimp uses its own palette, not the one used while Linrad is running.

Fig 19. Windows 98 on a 350 MHz PentiumII. Two different signals, separated by about 2 kHz in frequency and about 10 dB in amplitude are sent into the antenna connector of the receive hardware (WSE converters) The true signals are at about 37 kHz. The mirror image at about 62 kHz is rather strong because Linrad is not calibrated to suppress it. The ghost signal at about 83 kHz is a false signal. Windows 98 does not sample at 96 kHz - it actually samples at 48 kHz and delivers data to Linrad at twice the real sampling rate. When a signal is swept from 7002 to 7098 kHz, nothing is visible until the signal reaches 7026 kHz Two signals appear simultaneously. One at F for F=7026 to 7074 kHz, another at (F+48) or (F-48)kHz (one of them is outside the screen).

To SM 5 BSZ Main Page