|
The screen dumps on this page are all generated with the internal
signal generator of Linrad in a first instance of Linrad that is
set up to send the baseband over the network.
It is on the left hand side of the screen.
The keyed signal is 60 dB below the sweeping signal.
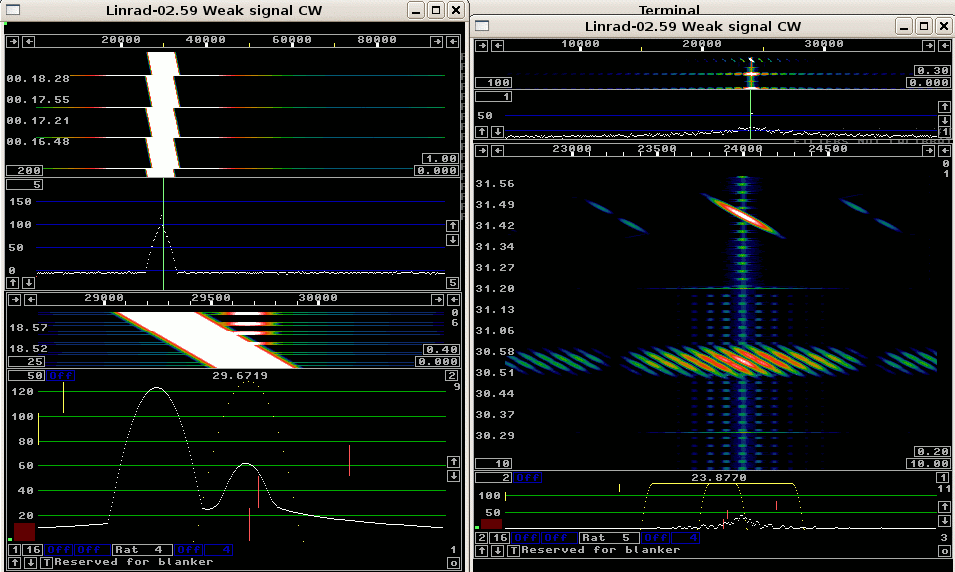
On the right hand side there is a second instance of Linrad reading the network data and displaying the waterfall graph. It serves as an analyzer of the signal that is used for the loudspeaker output of the first Linrad instance. Linrad-03.00 allows the user to select filtering in the frequency domain, the same method which was used in earlier Linrad versions. There is a new button in the upper right corner of the baseband spectrum which can take two values. When it is set to 1 filtering is in the frequency domain. By selecting 2 in this box, a FIR filter is used to make the filtering in the time domain. The FIR filter is designed to have the same frequency response as is obtained in the frequency domain filtering. The left hand side baseband filter has three different shapes in the three figures below. The window function is the Gaussian (N=8) for which the difference between the filtering methods is most pronounced. Figure 1 shows what happens when a single bin is selected for the baseband filter. It is obviously not a reasonable choice to use that for a filter in the frequency domain and it was not allowed in earlier Linrad versions. (They allowed minimum 5 bins, reasonable for the sin 2 window previously used.) With only a single bin selected, the reverse transform will always be a constant amplitude sinewave at the bin frequency. It does not matter whether the peak is actually at another bin. The sucessive back transforms generate the same frequency, but the phase jumps from transform to transform. The output is totally useless as can be seen at the right hand side baseband waterfall. The lower part, at time 30.55, is produced with the baseband filter in the time domain. The signal is split into several signals of similar amplitude. The upper part of the right hand side baseband waterfall shows the output from the FIR filter. The signal is perfectly clean as it sweeps across the passband. When writing this I do not know whether there will be any reason to retain the option to select frequency domain filtering in future Linrad versions. It seems reasonable to not allow it for filters that are not much wider than the bin response. |

|
|
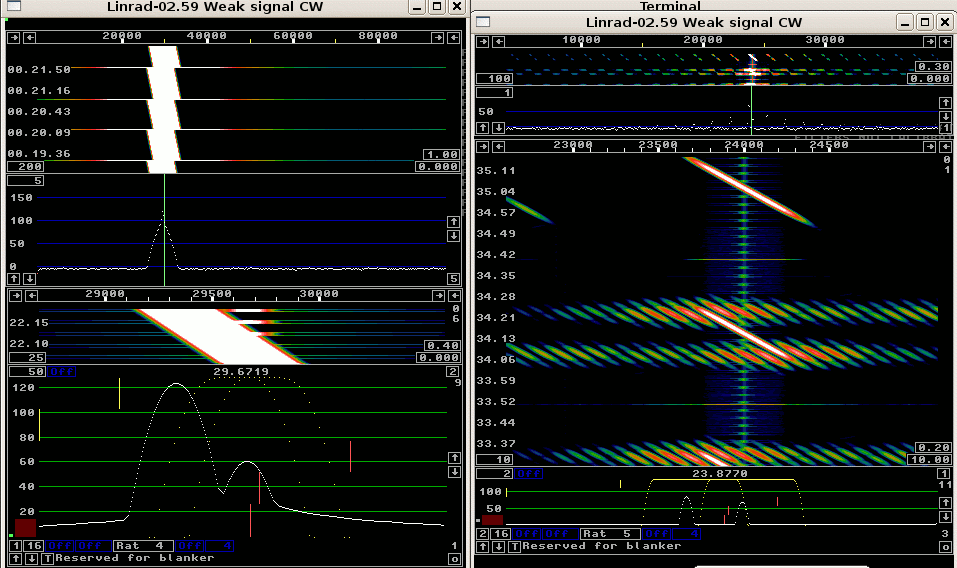
Fig 1. When a single bin is selected for the baseband filter (left) one must use time domain filtering. The right hand side baseband waterfall shows what happens if frequency domain filtering is selected. When the signal sweeps across the filter at time 30.55 it is the output of the frequency domain filter. Totally useless. The next sweep, at 31.45 is the output of the time domain filter. Figure 2 uses a baseband filter that is about three times wider than the bin response of the Gaussian window. For signals that are within the flat passband, the output is good, but signals that fall on the filter skirts become modulated. In real life one would not have strong interferences on the filter skirts so the ugly baseband signal for the frequency domain filter is not a problem. One would have to reduce the bandwidth or to tune for the interferer to be placed outside the filter anyway. |
|
|
Fig 2. A filter that is about 3 times wider than
the bin response provides a practically useful baseband signal
with the frequency domain filter.
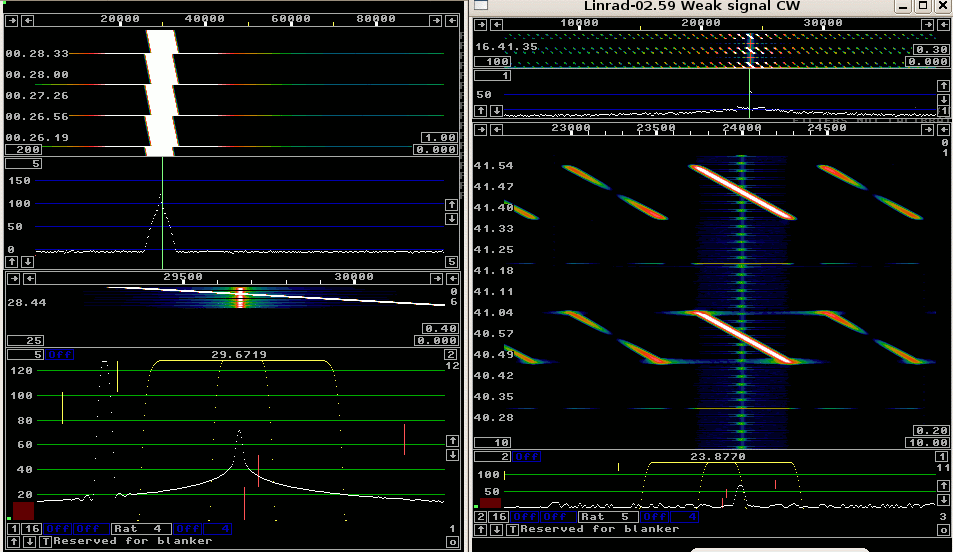
Figure 3 shows that the difference between time domain and frequency
domain filtering is small when wide filters are selected.
The reason for the introduction of a FIR filter in Linrad-03.00
is to allow shorter time delays through the baseband filter.
Earlier versions would require much larger fft3 transforms for a good
dynamic range.
|
|
|
Fig 3. Filters that are wide in relation to the bin bandwidth
work well both in the frequency domain and in the time domain.
To SM 5 BSZ Main Page |