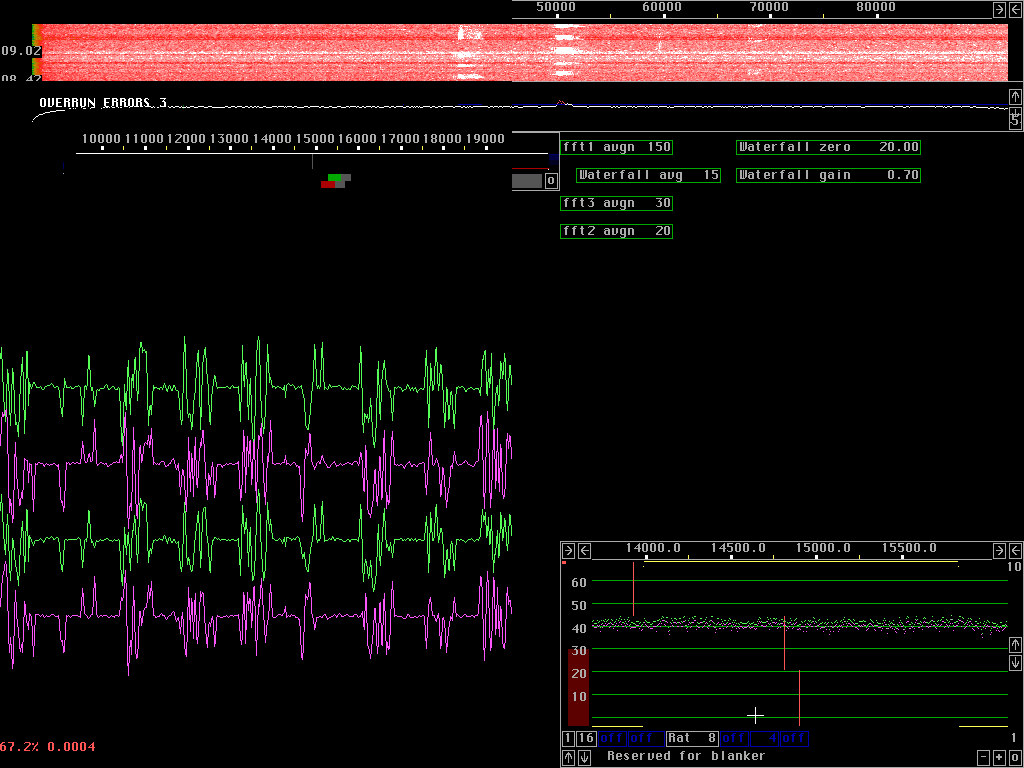
Fig 1. No blanker. Note that the powerline noise has short quiet periods.
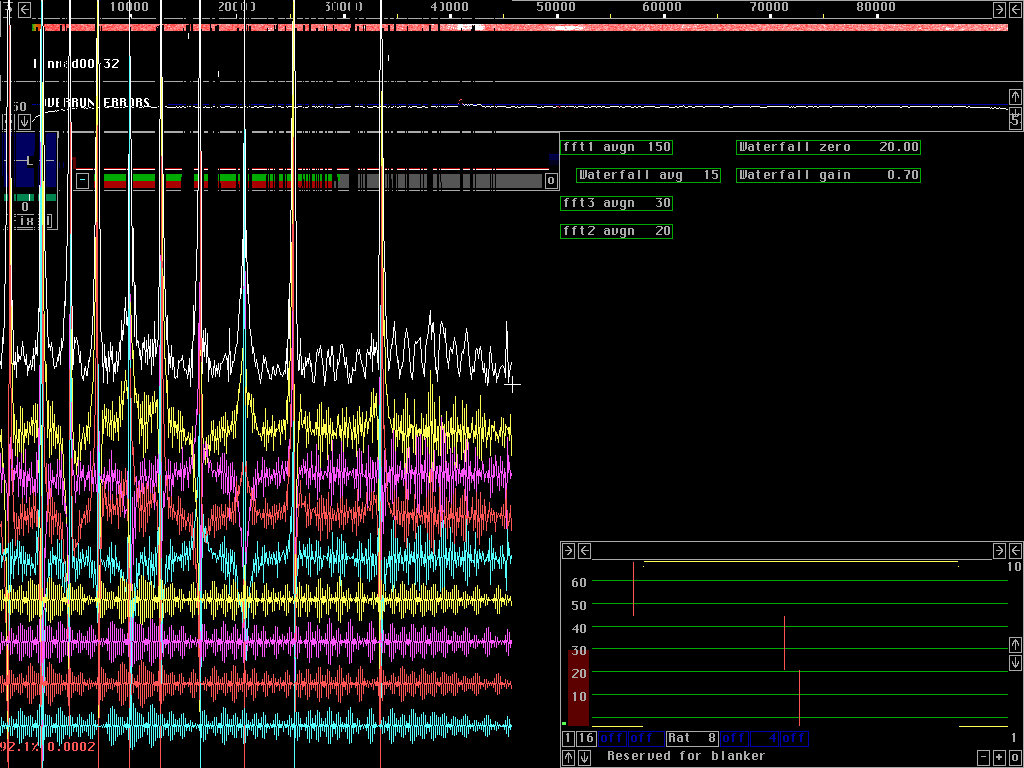
The Leonids 2001, many signals and severe powerline noiseFig. 1. shows the screen of linrad when the sequence is processed without any noise blanker. The noise floor is raised by about 25dB so it is approximately at S9 with a conventional S-meter with 3dB for each S-unit.
|
|
All screen dumps on this page show the same sequence.
For this page linrad00-32 is used.
This version has some improvements in the blanker algorithms
that make the performance slightly better compared to earlier
linrad versions.
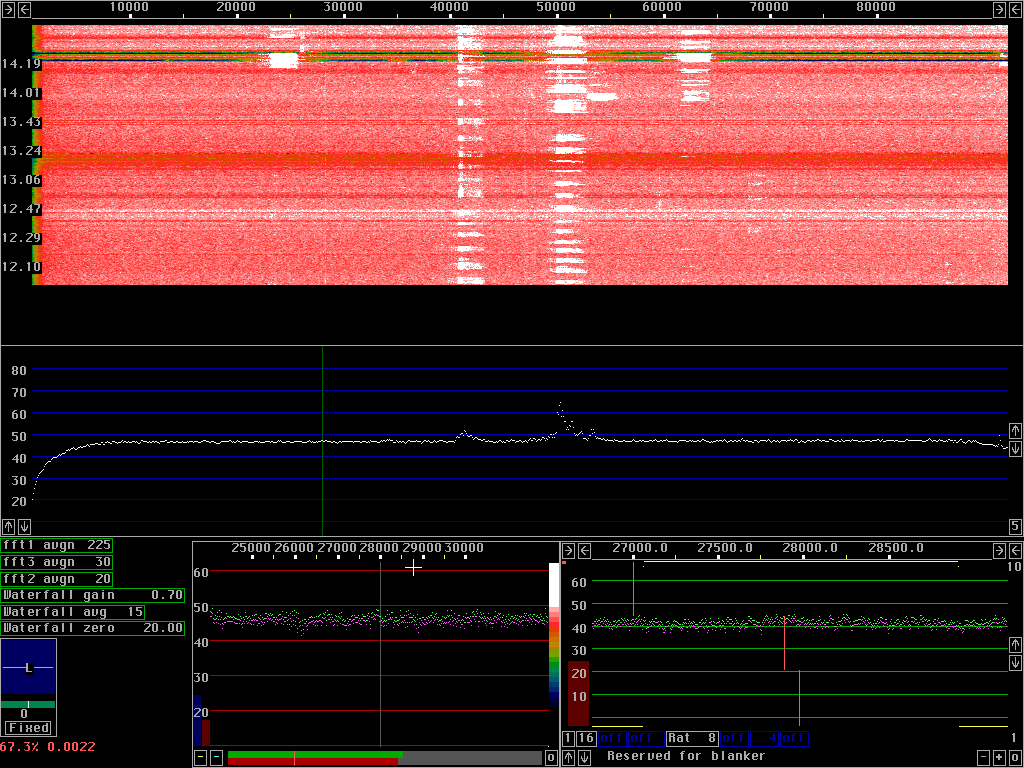
In fig. 2. the processing is stopped during one of the short
quiet periods which is a clear demo of the high power line
noise level.
|
|
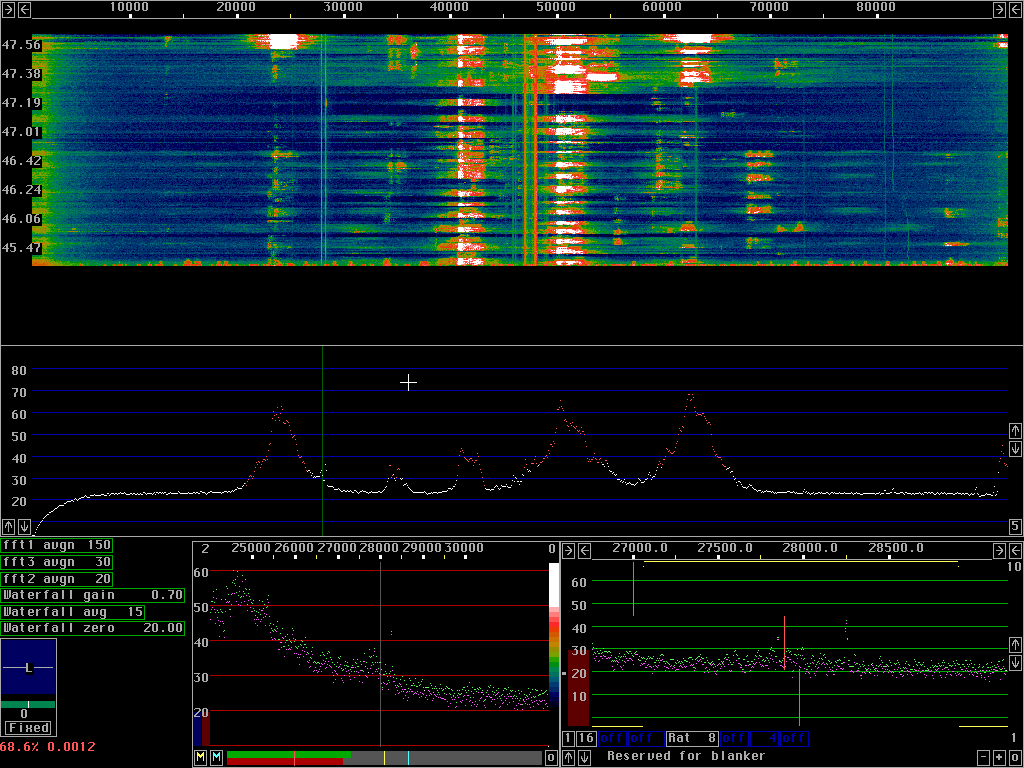
Fig. 3. shows the blanker in proper operation with both
steps enabled, both the smart blanker and the dumb blanker.
I do not have a modern transceiver with a good noise blanker in it
so I can not tell how linrad compares to conventional
noise blanking, but compared to my old FT221 linrad is much
better.
|
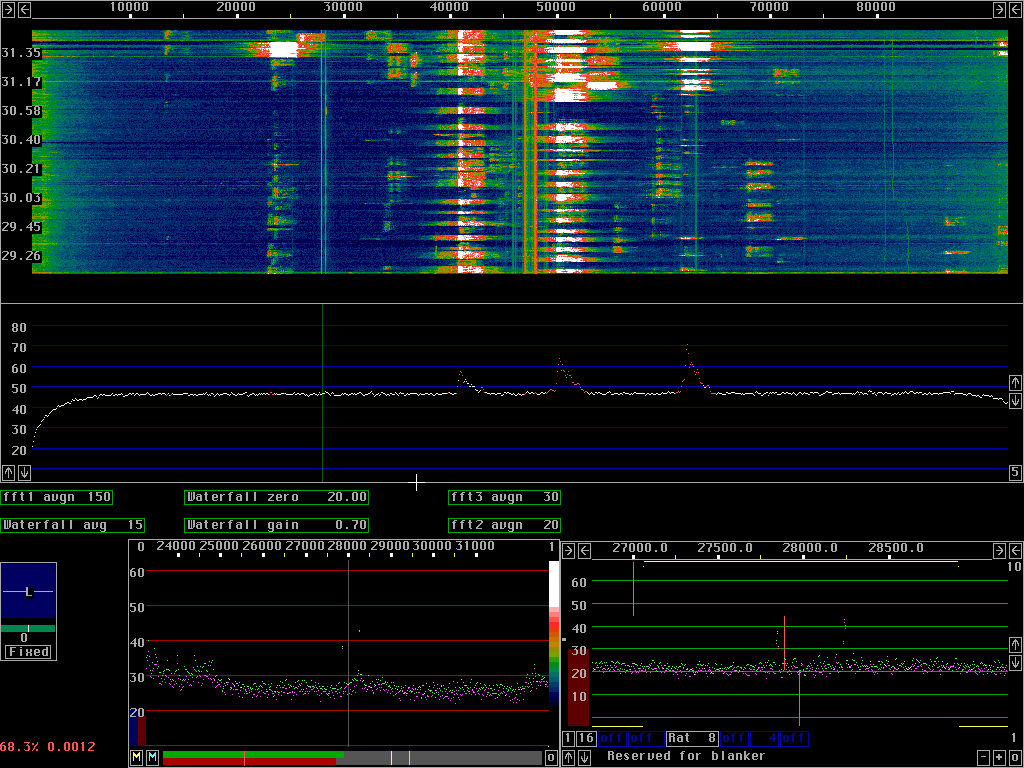
Excluding frequencies.The main spectrum (blue dB scale) is used for a first search for strong signals. This spectrum is searched in two ways, fast and slow. The average is calculated in two steps, first the number of spectra indicated in the little box in the lower right corner is scanned for signals that are strong enough to possibly saturate further processing. For the processing on this page the first fft resolution is 300Hz with a sin to power 3 window so the average of 5 spectra is computed in about 15 milliseconds. The main spectrum averaging number is 150 so it represents the average over about half a second. The slow average is searched each time 5 new spectra are included so signals well above the noise floor are detected much quicker than in 0.5 seconds.The blue vertical bar at the left side of the high resolution graph sets the S/N level at which signals are excluded. This level can be set lower if long averaging times are used because then the noise floor becomes flatter. Searching for signals in the main spectrum does not work well in situations with continuous powerline noise as one can see from a comparison between fig. 2 and fig. 3. The powerline noise has lifted the noise floor by about 25dB so only signals that are more than about 25dB above the white noise floor can be found by use of the main spectrum. The most recent line of the waterfall graph is used for a second search for strong signals. Here noise pulses are not present any more so much weaker signals can be found in a difficult situation as the one used for this page. The S/N level for deciding if a frequency shall be excluded when searching the high resolution spectrum (fft2, the last line of the waterfall) is set by the red vertical bar in the high resolution graph. How to set this level depends on the waterfall averaging chosen. All spectrum points that are considered to contain strong signals are red in the main spectrum. The red and/or blue bars are set too low if red points occur at frequencies where there is no signal. Exactly how to set these levels for optimum performance is unclear at the moment. I need several more difficult test cases to get some experience. Maybe it is quite different on crowded HF bands compared to nearly quiet VHF bands as one normally has during EME operation. Excluded frequencies are not rejected, they are just passed outside the noise blanker and added to the blanked signal. In case the amplitude is very large, the excluded frequencies are attenuated to prevent saturation in the high resolution fft which uses 16bit only to take advantage of the very fast MMX (multimedia extension) instructions of modern processors.
Effects of the blanker on excluded frequenciesTo show what happens to excluded frequencies, a part of the spectrum from 67kHz to 82 kHz is artificially excluded. Fig. 4 shows the dumb blanker works in this situation. As one would expect, the excluded frequencies contain the powerline noise as if no blanker was present at all, but other frequencies are nearly free from the powerline noise.
|

|
The smart blanker that subtracts a pulse with the shape
that is given by the pulse response of the hardware
behaves differently for excluded points.
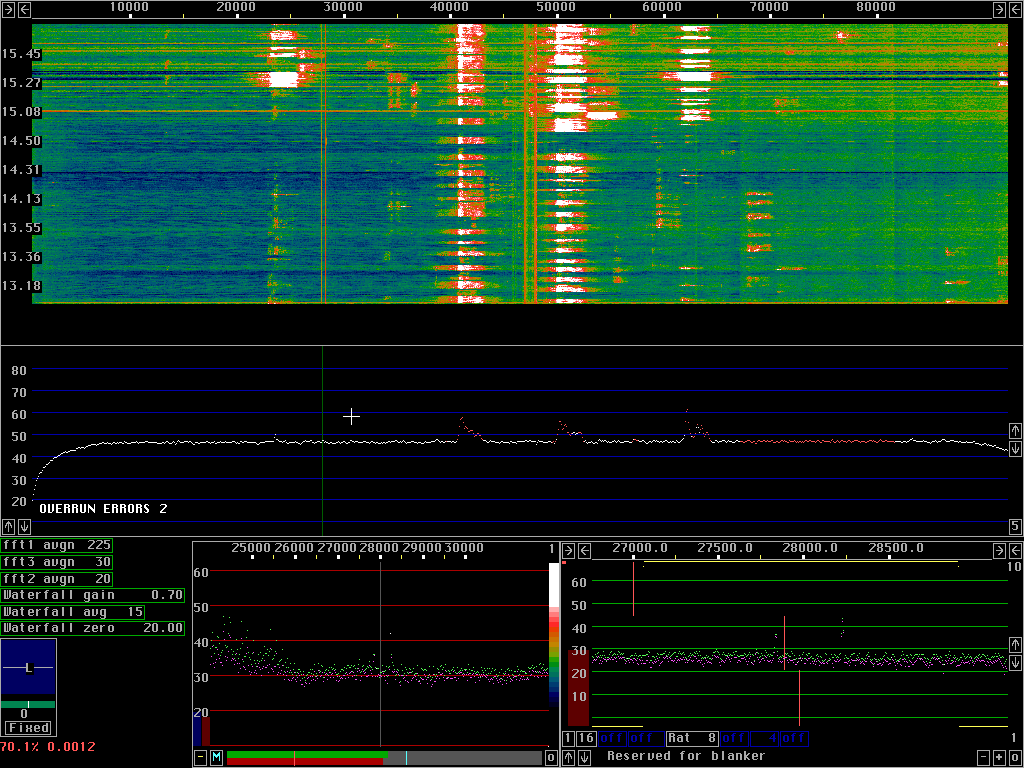
Fig.5 shows what happens if only the smart blanker is
operated on excluded signals.
|
|
Since a reference pulse is removed with the pulse shape
it would have if no points were excluded, the signal does not
become zero during the time of the pulse.
What remains during the pulse time after subtraction of the reference pulse
is a smaller pulse that will cancel the pulse present in the
excluded frequency range.
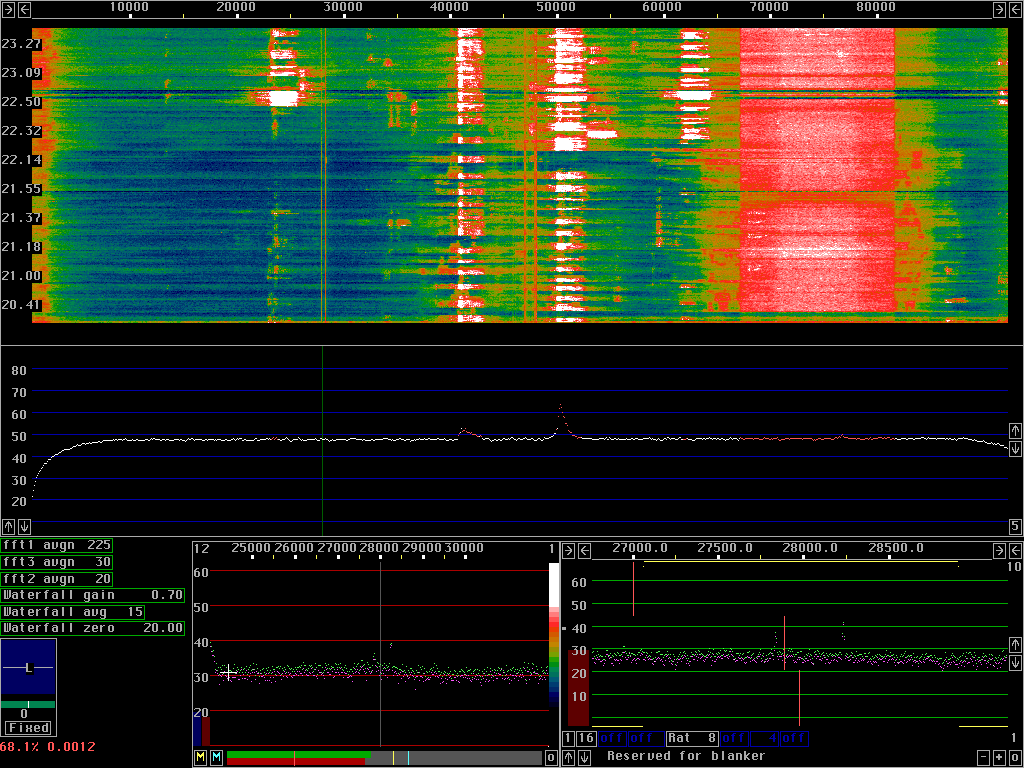
Under normal operation the dumb blanker is operated after the smart blanker. If the threshold of the dumb blanker is set very low and if many points are excluded, the dumb blanker will clear points which actually constitute correct data produced by the smart blanker to cancel pulse energy in the excluded frequencies. Fig. 6 shows both blankers running with a too low level for the dumb blanker.
|
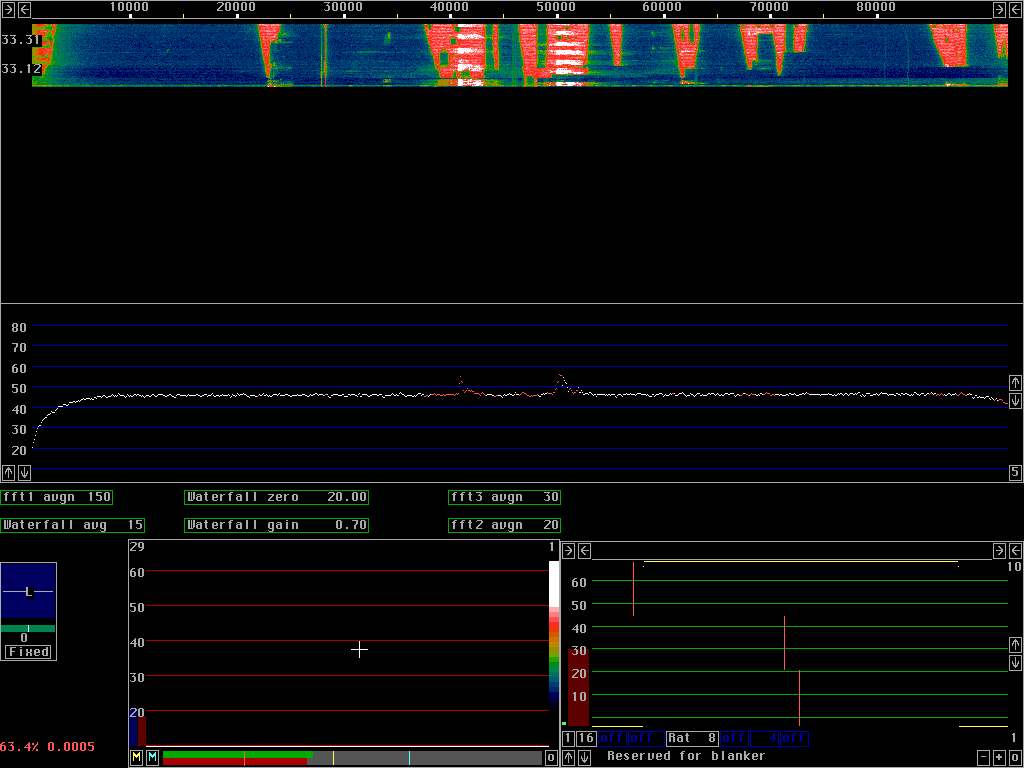
Practical considerationsWhen experimenting with the blanker it is a good idea to select minimum size for the baseband fft (fft3) in order to have a fast response on parameter changes. Listen to the desired frequency and adjust all four blanker controls for best S/N.Setting controls too high is safe but will not give optimum performance. If the blue vertical bar is too low for the fft1 averaging chosen, points will be excluded due to random variations in the noise floor. This is easily detected in the main spectrum, red points that have no corresponding signal in the waterfall graph. To look for this phenomenon, disable the dumb blanker because it generates signals in the excluded frequency range. If the red vertical bar is too low and the dumb blanker is operating with a low threshold, random frequency bands with artificial strong signals are produced as shown in fig. 7.
|
|
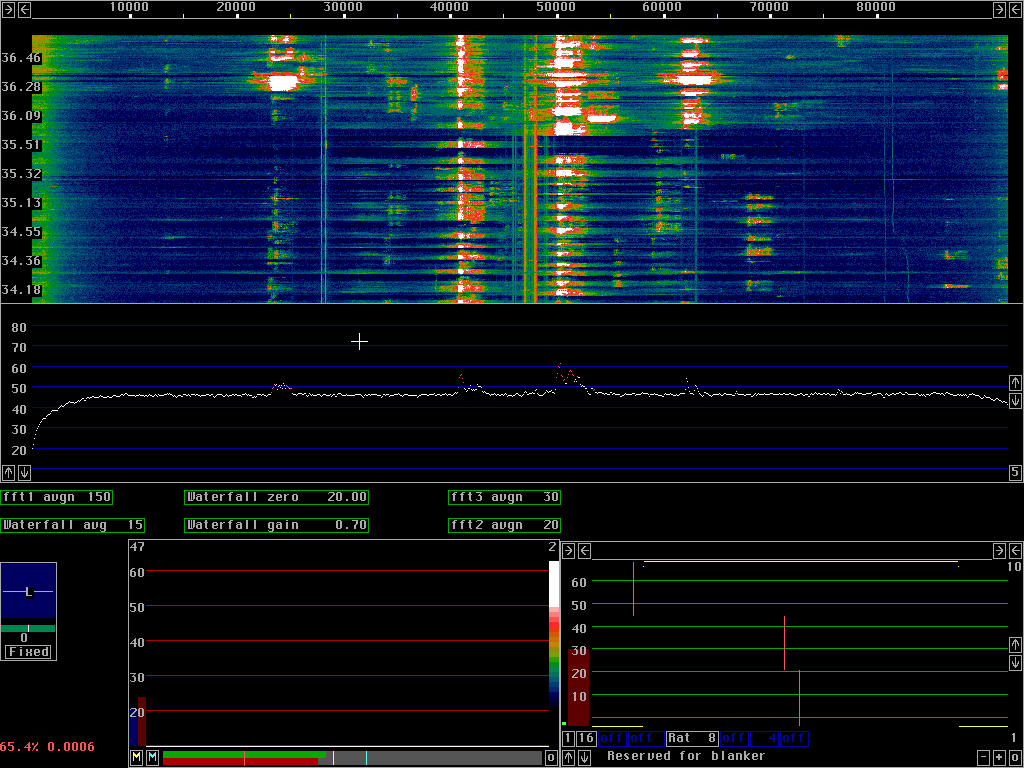
Blanker levels may be set too low causing severe loss of data.
This error is shown in fig. 8.
|
The time functionsTo assist in understanding the blanker operation linrad has oscilloscope functions. The two groups of signals, the weak signals on which the blanker operates and the excluded frequencies, the strong signals, are displayed by a mouse click on the little box with an "o" in the lower right corner of the high resolution graph. Fig.9 shows a typical example from the data used for the images on this page.
|
|
The benifit of using large bandwidth for the blanker is clearly
demonstrated by fig. 10.
The noise blanker is improved in linrad00-32. Further improvements are possible but to investigate what can be done I need test recordings from interference situations where the current blanker does not work well. The demo on this page is showing SSB signals. CW signals are much easier to find. The optimum way of finding what frequencies to exclude is hard to figure out because circumstanses may differ dramatically depending on the frequency band. Linrad still has only the mode for weak CW implemented. It is really going outside the intended usage to open the bandwidth to allow ssb reception but it works quite well and is a good test for the algorithms. In other modes there is no need for very large fft's on the entire spectrum so it will be possible to use more efficient methods for the noise blanker. Splitting the signal into more than two and making more independent transforms on these signals will make it possible to suppress pulse noise even better.
|