Path modulationWhen the weak CW signal arrives at the other end of the signal path, the spectrum is distorted because of multipath propagation and other phenomena.When the bandwidth of the received carrier is much smaller than the bandwidth of the sidebands carrying the information, the carrier can be detected long before the signal is strong enough for a conventional receiver.
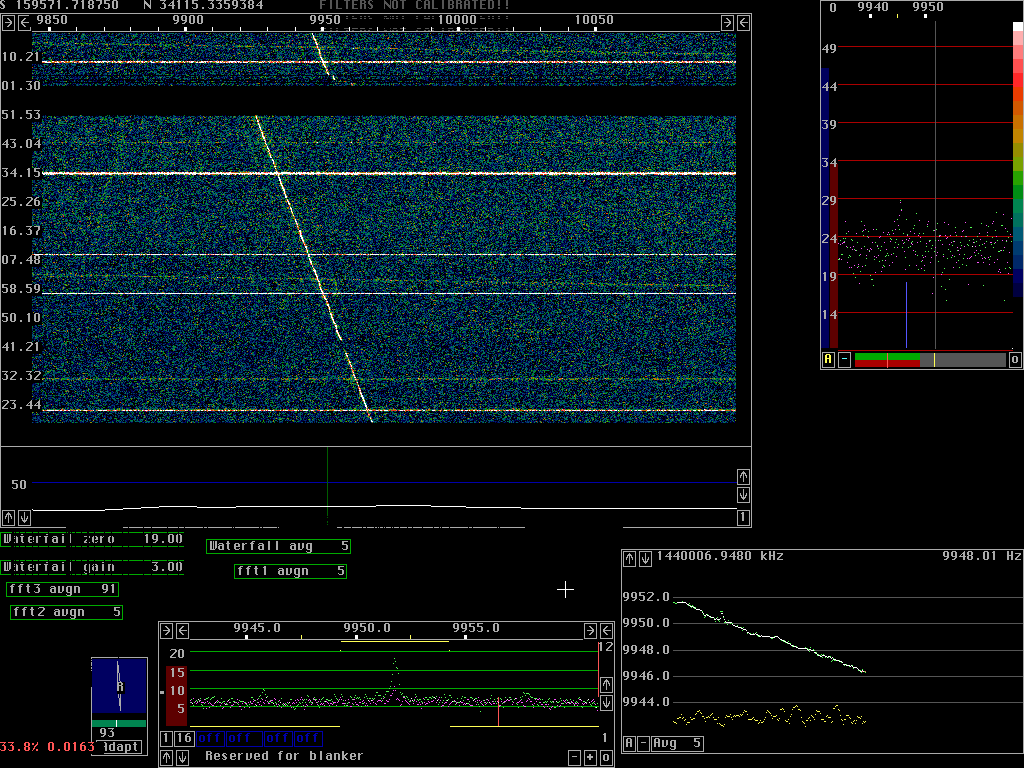
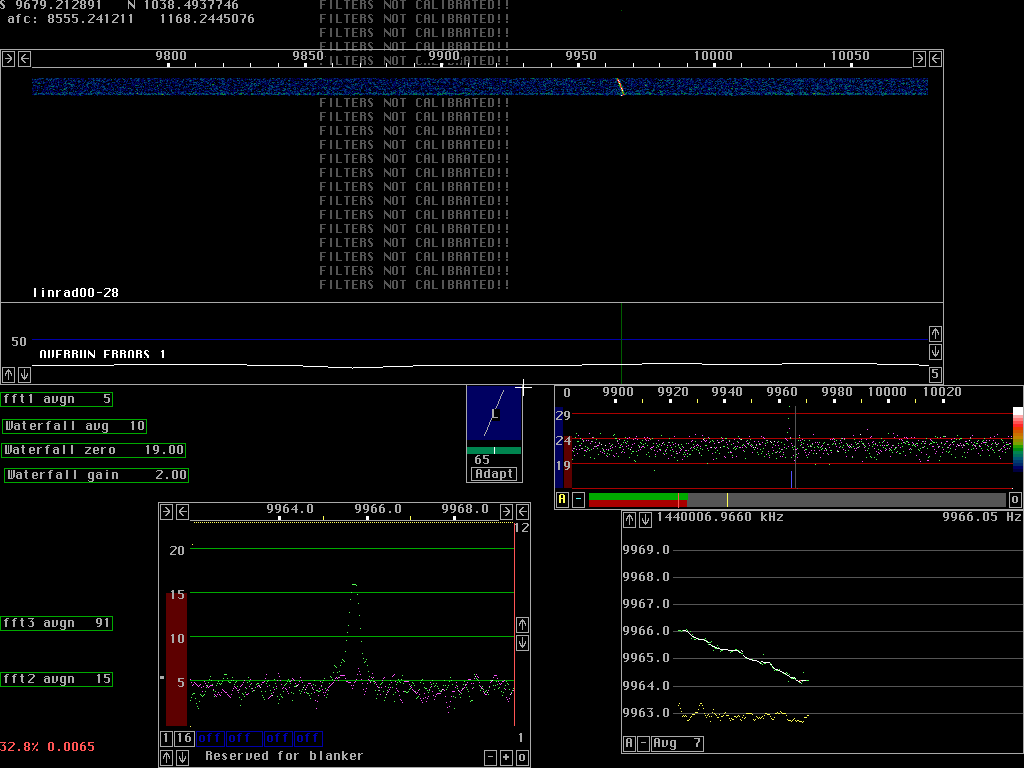
A highly stable but very weak signal on 144MHzFigure 1 shows a 144MHz transmission from KO6RS made Oct 3 1999. The transmission lasts for one and a half hour. Part of it is carrier only and part is morse code with a single message repeated many times.In fig. 1. The signal is shifted to the baseband by an AFC that uses the frequency determined from the average frequency over 17 seconds. The bandwidth of the baseband signal is about 0.25Hz and the average S/N is about 12dB. Fig 2 shows a few minutes at the beginning of the transmission. In fig 2 the carrier is unmodulated so the transmitted power is nearly 3dB higher and no energy is present in the sidebands. The average S/N is about 17dB in 0.25Hz bandwidth. The carrier bandwidth is determined by the transmission path, the fft has much higher resolution. In case the CW signal had been received in 18Hz bandwidth as would be the case in an optimised conventional receiver, the average S/N would have been -6.5dB. In order to receive CW by ears while using a matched filter the momentary S/N has to be about 9dB. The difference between the average S/N and the momentary S/N is in the range 4 to 7 dB. The signal produced by KO6RS is thus about 10dB below the level that can be copied by ordinary means.
|
Coherent averaging of CW signals is a way of improving the S/N for a signal that is too weak for any information transfer by listening to the transmission even if the message is repeated many times.
The advantage obtainable by use of coherent integration depends on the path modulation since the narrowest bandwidth one can use is determined by the bandwidth of the received carrier. It is obvious from fig. 1 that the carrier phase can be extracted with good accuracy most of the time.
To extract the carrier phase with good enough accuracy one would need a S/N of something like 8dB. This is the peak level required during qsb peaks which means that the average level of the carrier has to have S/N around 3dB in 0.25Hz bandwidth. This should be enough to discover an unknown signal and lock to it with a very slow AFC. The detect threshold for coherent averaging is thus about 9 dB below the level shown in fig.1 or about 19dB below the threshold for ordinary CW.
To decode the signal from KO6RS one would like a S/N for the information somewhere around 10dB which means one would have to gain about 13.5 dB by averaging. (There is a 3dB advantage from knowing the phase, coherent CW). This means that the morse code message will be received after 22 repetitions have been accumulated which would take something like 3 to 5 minutes.
Now, since the amplitude is not constant, it is not very clever to include the parts of the transmission where the signal is very weak since then one adds noise only. Using the amplitude of the carrier as a weight factor in the coherent averaging one will gain something like a factor 2 in speed which means that 2 minutes would probably be sufficient.
What time it would take to receive a message at the detect threshold is difficult (for me) to estimate, but as a minimum one would expect 20 minutes and maximum probably less than one hour.
The signal level of KO6RS would be 7dB S/N in 2.5Hz bandwidth when carrier only is transmitted. I do not know what S/N is needed for PUA43 but since it evaluates but since it uses 43 tones I would guess the S/N for each channel has to be about 6dB stronger compared to using a single tone. Assuming the required S/N is 13 dB, PUA43 has to gain 6dB by integration which means that the integration time has to be 16 times the time constant of a 2.5Hz filter or 6 seconds. A complete message would need something like 10 times as much or 1 minute. Of course one can not receive a message via EME in 1 minute with PUA43 because of the qsb. The signal level is most probably near zero now and then due to the qsb so some information will be missing. For weaker signals where the long times will average out the qsb the 1 minute should be a reasonable starting point.
Of course PUA43 can be used for even weaker signals, but because of the incoherent averaging, time grows quadratically. Since a qso means the transfer of at least 2 messages in each direction, the practical limit for PUA43 is not much different from the limit for coherently averaged CW.
None of the methods is in practical use yet (Oct 2001) but PUA43 has been demonstrated while coherent averaging is not yet demonstrated practically. It remains to be seen if the estimations on this page are reasonable or if I have made some serious mistake. If the information is essentially correct, coherent CW will be a much better weak signal mode than PUA43 for 144MHz EME.
It is obvious that much better methods can be developed. The main disadvantage of PUA43 is that it uses too high bandwidth. PUA43 also has difficulties for random contacts in that one has to guess where the other station might be located and then evaluate with the doppler shift variation that follows. At an integration time of 1 hour the doppler varies by typically 20Hz so one would have to evaluate for maybe 25 different locations simultaneously.
In the future it will be possible to develop better methods for
digital low level EME.
Just by changing the morse code definition like this:
dit = 2 time unit
dah = 4 time units
space within character = 1 time units
space between letters = 2 time units
one will get about 3 dB more carrier power because of the
higher average power.
The ugly morse code can still be copied by ear by stations
having big enough antennas so compatibility is not lost.
If heat in the tx transistor amplifier is the limiting factor
it is not a good idea!
Some multi tone coding with 0.25Hz bandwidth should be optimum and about 10 times faster than PUA43.