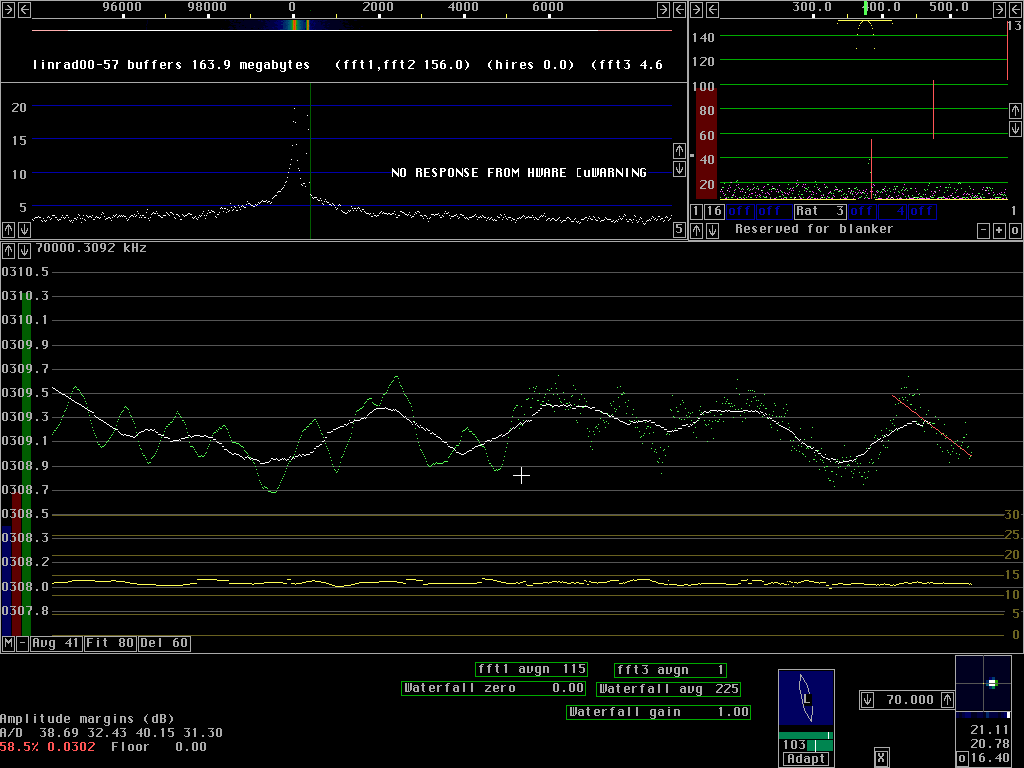
Windows and filteringWhen producing an average power spectrum by taking the straight average over N points, we do a low pass filtering. Look at a single frequency F. We denote the corresponding power level, the power contained in the FFT bin belonging to F by P(F,t) where t is the time of arrival of the transform. When we form the average of N transforms asPavg(F,t+N/2) = [P(F,t)+P(F,t+1)+P(F,t+2)+. . . . .P(F,t+N-1)] / N the new series of power values for the frequency F will be much smoother. A filter like this is not particularly good however, it is a low pass filter with the lowest possible cut off frequency but it is not very steep. By multiplying the individual power values with a window function that makes the weight of the first and the last power level small, it is possible to make a steeper filter but the cutoff frequency will be higher. It is exactly as with the window functions used with fourier transforms. To illustrate what happens when the window is selected or deselected Fig. 1 is produced with unusual AFC parameters that make the phenomenon clearly visible. The signal is a weak carrier that is very close to a noise modulated signal. The second fft is disabled and the first fft is run at a bandwidth of 60 Hz. A signal that is only 10 dB above the noise, (S+N)/N = 10 dB will have a contribution of 10% noise at the peak and therefore the position of the peak can not be accurately determined. By forming the average over 41 transforms the peak position can be determined within about +/- 0.5 Hz as can be seen from the green curve of figure 1. The left half is averaged with the window enabled and the right half is averaged with the window disabled. One can clearly see that the window helps to suppress fast variations with time in the averaged power spectra. The white curve does not change however. Fitting a straight line to the green points is equivalent to cascade another low pass filter and that removes the relatively weak noise from the green curve. If the frequency variation had been caused by path modulation or poor frequency stability it would be desireable to track the green curve. One would then disable the line fitting by setting the "Fit" parameter to 1 or make its corner frequency similar to that of the averaging process by setting it to about half the value of the "Avg" parameter. In such a situation the windowed averaging is probably much better than the unaveraged one because the slow variations of the frequency are real while the fast variations are caused by white noise. Avoiding to frequency modulate the signal by noise may me important for subsequent processing stages if coherency is used one way or another.
|
| To SM 5 BSZ Main Page |