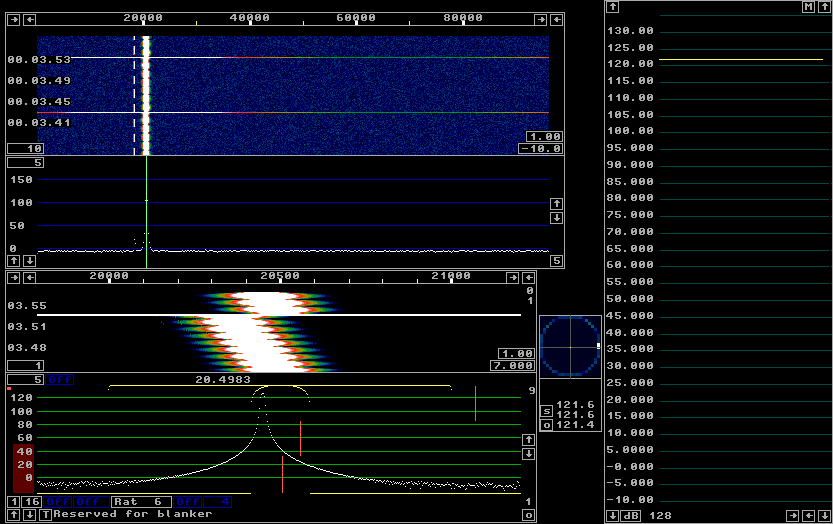
Fig. 1. The internal signal generator of Linrad. The amplitude of the dominating signal is 0x7e00 (32256 digital) which is 98.4% or about 0.2 dB from saturation. The main signal is at 121.5 dB.
 Fig. 1. The internal signal generator of Linrad. The amplitude of the dominating signal is 0x7e00 (32256 digital) which is 98.4% or about 0.2 dB from saturation. The main signal is at 121.5 dB. |
|
|
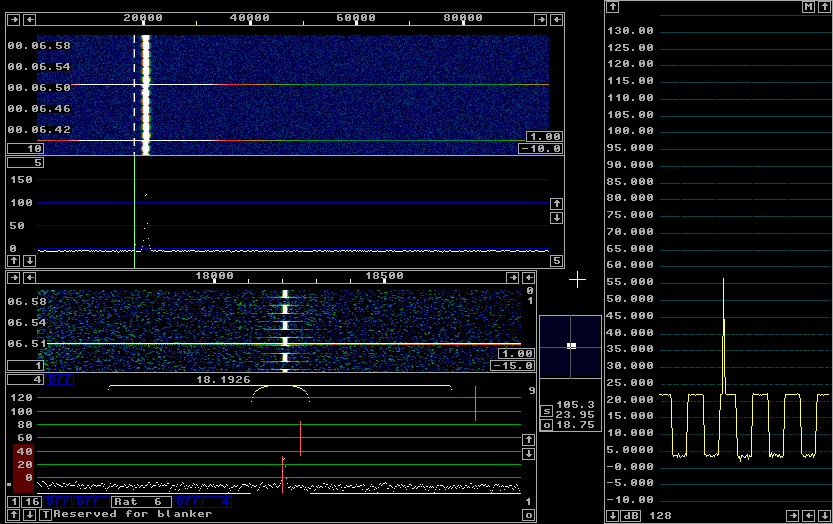 Fig. 2. The weak signal, 100 dB below the dominating signal is on/off keyed. |
|
As can be seen from figure 2 the weak signal is at its expected position in the S-meter graph. The noise floor is at about 3.5 dB in 1 kHz bandwidth which corresponds to -148 dBc/Hz. As it happens, the noise floor of a modified Delta 44 is very close, -148.5 dBc/hz. Using it at 16 bit only should result in about a 3 dB loss of dynamic range since the sum of two uncorrelated noise levels is 3 dB above each individual noise level. in real life, truncating the 24 bit data of the Delta 44 to 16 bits causes a dynamic range loss of 2.2 dB as can be seen in fig. 1 here The Linrad network. Truncating to 18 bits means that the Delta 44 noise is degraded by the addition of an uncorrelated noise source that is 12 dB weaker with an associated dynamic range loss of about 0.2 dB. Truncation and rounding.Figure 3 shows what happens when the internally generated signal is truncated to 15 bits. |
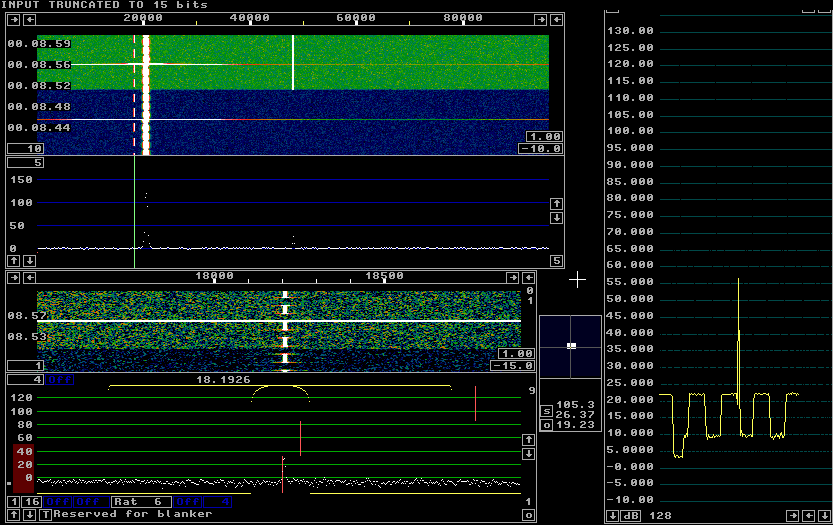 Fig. 3. Truncation from 16 to 15 bits. |
|
As one should expect, the noise floor rises by 6 db, but there is also a spur at the passband center. Truncation by 1 bit means that 1 is subtracted from all odd numbers while all even numbers are left unchanged. 50% of the data points are odd and therefore 0.5 is subtracted on the average. The consequence is a signal with an amplitude of 0.707 (0.5 in both I and Q) at frequency zero. The center spur would disappear if 0.5 were subtracted from each I and Q sample in the conversion to floating point that is done before the data is used. Linrad currently does not add any such correction but it might be appropriate to add it for e.g. the SDR-14 which only transfers 16 bits of data. In linrad-02.55 and earlier versions no attention is paid to DC shifts that might be introduced by truncation. The internal generator uses rint() to round to the nearest integer when all 16 or 32 bits are used. When the user selects truncation, the function floor() is used instead to round to the integer below. This way the spur shown in figure 2 is avoided in linrad-02.55. VHF-sampling receivers.A radio that samples at VHF uses digital technology to shift the signal frequency to the baseband. To do that it uses two (digital) mixers in quadrature to generate I and Q. With appropriate filters the signals outside the region of interest are removed to allow sending the signal to the PC at a greatly reduced sampling speed without problems with aliases.The digital section of radios like SDR-14, the Perseus HF receiver, QS1R, SDR-IP and others use many bits in their internal digital processing. The number of bits actually sent to the PC can be lower without loss of dynamic range (or rather with a permissible loss that is only a small fraction of a dB.) Even more important would be to not save more bits than actually needed to the hard disk when recording wideband data. Figure 4 shows the Linrad screen with a 32 bit signal generated by the internal generator. The signal has the same general characteristics as the signal used for the 16 bit example above. The 32 bit signal in figure 4 has a sampling rate of 1 MHz. |
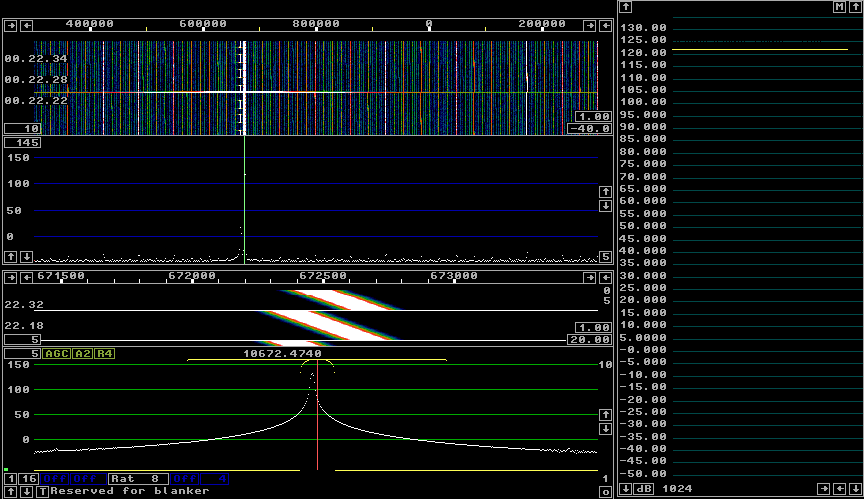 Fig. 4. The 32 bit signal at 1 MHz. All the spurs are caused by rounding errors in the FFT computations. |
|
The dominating signal in figure 4 is at 121.5 dB exactly as in figure 1. It has the same amplitude relative to saturation. Figure 5 shows the keyed weaker signal. |
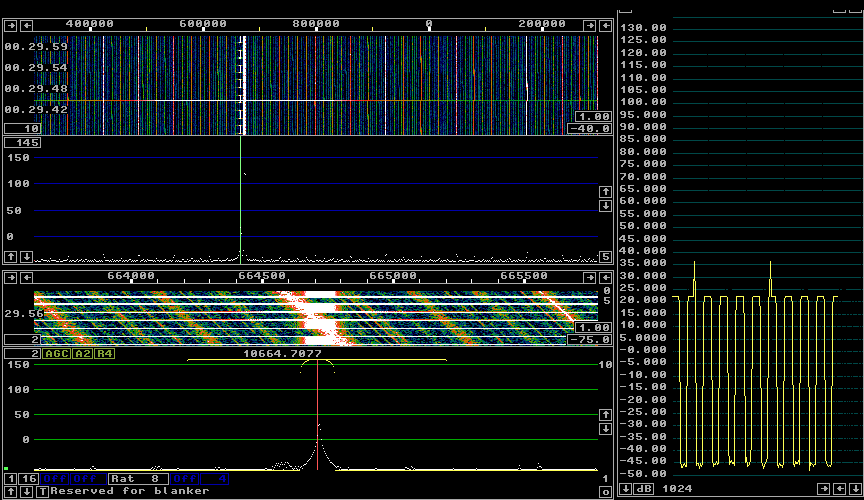 Fig. 5. The FFT procedures do not have the number of bits required to show the quantization noise of a 32 bit signal. The limitation to the dynamic range is the spurs generated by the FFT. |
|
The quanitzation noise in figure 2 is at about +3.5 dB on the S-meter. The sampling rate in figure 5 is 1 MHz while it is 96 kHz in figure 2. 10 times higher sampling rate means 5 dB lower quantization noise. 16 more bits places the quantization noise of the 32 bit signal at -97.5 dB. The S-meter shows a noise floor of -46 dB. Very much higher. The first step of the FFT processing in Linrad is conversion from 32 bit integers to 32 bit floating point. This means that the signal is truncated to 24 bits, the floating point format uses 8 bits for the exponent. Taking this truncation into account would place the quantization noise at -65.5 dB. Rounding errors create spurs and noise that places the noise floor about 20 dB higher at the particular frequency where the keyed signal is placed. Figure 6 shows the Linrad screen when the 32 bit signal is rounded to 18 bits only. The noise floor is at -18.5 dB which means that the quantization noise is at -170 dBc/Hz. |
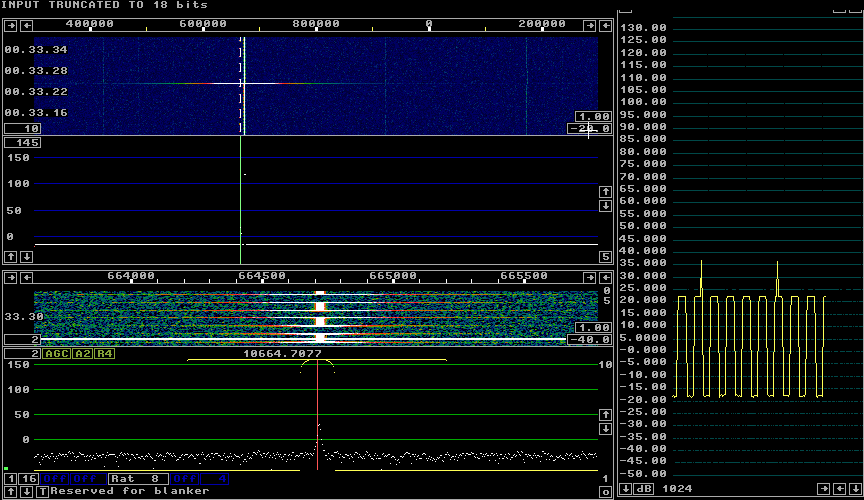 Fig. 6. Truncating to 18 bits lifts the quantization noise high enough to hide the spurs caused by the limited accuracy of the FFT at a sampling speed of 1 MHz. |
|
The noise floor of the Perseus HF receiver is at -151 dBc/Hz when using all 22 bits transferred over the USB (at large frequency separations.) It is obvious that saving 18 bits of data at 1 MHz as is done in Linrad is overkill. On the other hand, saving only 16 bits at 1 MHz would place the quantization noise only 7 dB below the noise of the Perseus itself causing a loss of dynamic range of about 1 dB. At 2 MHz, the quantization noise would be 3 dB lower so saving 16 bits only as is done by perseus.exe will cause a loss of 0.5 dB only and that is a very reasonable loss in relation to the advantage of saving data in the standard format of a 16 bit .wav file. At 125 kHz 1.5 more bits are needed to place the quantization noise equally far below the Perseus own noise compared to 1 MHz. Figure 7 which uses the internal signal generator of Linrad at 125 kHz shows that the spurs generated by the FFT procedure have the nice behaviour to be about 9 dB lower than at 1 MHz so truncating to 19 bits produces the noise level required to hide them 3 dB better as compared to figure 6. It is obvious that saving 18 bits of data is adequate for the Perseus even at its lowest frequency and that the 22 bit format used in the USB transfer is perfectly adequate with a broad margin. |
 Fig. 6. At 125 kHz the spurs caused by the FFT are about 6 dB lower than at 1 MHz so truncating to 19 bit produces enough noise to hide them. |
|
The current status of Linrad is thus as shown in table 1. Sampling Max number Noise frequency of bits floor 4 MHz 17 -170 dBc/Hz 1 MHz 18 -170 dBc/Hz 250 kHz 19 -170 dBc/Hz 68 kHz 20 -170 dBc/Hz 17 kHz 21 -170 dBc/HzLinrad limits the dynamic range by generating spurs in the FFT computation due to rounding errors. There is no need to improve the FFT accuracy until hardware with a noise floor below 157 dBc/Hz becomes available. The dynamic range in the usual bandwidth of the amateur community (500 Hz) would then be 130 dB. It will be very hard to design such a radio that is reasonably free from spurs down to 130 dB below a near saturating signal so upgrading the Linrad FFT may never become meaningful. Transferring more bits than those listed in table 1 might also never become meaningful. To SM 5 BSZ Main Page |