Another optimised antenna was given by Longsomboon,
Green and Cashman [8].
For this antenna, using only 5.2 mm elements,
I have included the ohmic losses in all calculations.
Gain vs frequency is given in fig 2 and physical dimensions in table 6.
When this antenna is used as the initial antenna,
the brute force method produces a false optimum,
that uses one element less than the initial antenna, fig2 and table 6.
The iterations are stopped when no further improvement is possible,
which happens when the unused element is short enough to
have no influence.
By removing the very short element, the false optimum
8 element antenna becomes an optimised 7 element yagi.
By adding a director at a normal position in front of
this 7 element yagi, a new initial antenna is obtained.
Again running the brute force optimisation gives the long
optimum antenna of table6 and fig 2.
The gain improvement over the design of Longsomboon et al is 0.8dB.
This comparison is unfair, since the boom has become much longer.
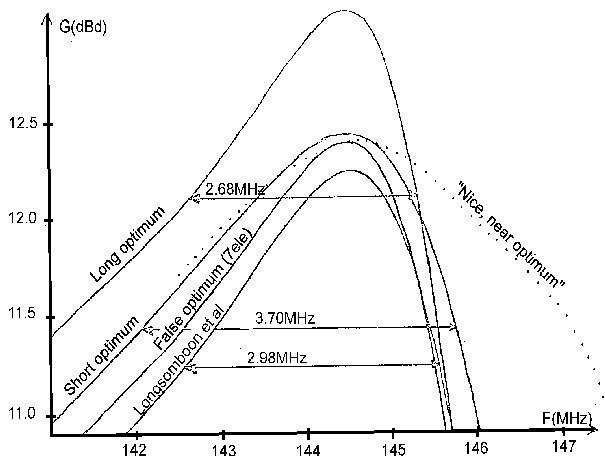 Fig 2. Gain above dipole vs frequency for the 8 element design
by Longsomboon, Green and Cashman, compared with 8 element
optimum antennas produced by the brute force optimisation method.
The intermediate 7 element design is also shown, see text. -1 dB
gain bandwidth is indicated.
Fig 2. Gain above dipole vs frequency for the 8 element design
by Longsomboon, Green and Cashman, compared with 8 element
optimum antennas produced by the brute force optimisation method.
The intermediate 7 element design is also shown, see text. -1 dB
gain bandwidth is indicated.
For long yagis the practical optimum antenna is the best antenna
at a certain boom length rather than the antenna using the
smallest number of elements.
Anyhow this antenna is the optimum 8 element yagi with
element diameter 5.2mm.
Slightly more gain can be obtained by increasing element
diameter and/or replacing aluminium with copper.
Adding one normal director 0.1 meter in front of the radiator
of the false optimum antenna,
removing the unused one, forms another initial antenna.
Running the brute force optimisation on that produces
the yagi named "short optimum" in table2, and fig 2.
Comparison with the design by Longsomboon et al shows that
the gain has increased by 0.19dB (4%), the bandwidth is
increased by 25% while the boom length is reduced by 4%.
Attempts to add more elements between the others were not
successful, i.e. initial antennas with a 9th element
inserted loose one element and come back to the short optimum.
8. CONTROLLING IMPEDANCE AND OTHER PROPERTIES
The optimisation procedure is the simultaneous minimising
of several functions of the antenna geometry.
We are free to add more terms into the sum of squares,
and with suitable weight factors it is possible to control
to what extent these terms contribute to the sum of squares.
Two natural things to add to F(x) are cz*(Re(Z)-50)*(Re(Z)-50)
and cz*Im(Z)*Im(Z).
These terms are zero when the feed point impedance
is 50 ohms resistive and hence the optimisation now will
tend to give 50 ohm antennas.
If 50 ohm feed impedance can be obtained with only
a small loss of gain, a very small value on the coefficient
cz is required.
Different values of cz will give different compromises
between gain and feed point impedance.
In this way the optimised 50 ohms antenna in table2 is obtained.
The loss of gain is only 0.01dB, and the frequency response
is about 7% narrower.
One more term that I like to add to F(x) is cl*(ohmic losses squared).
The reason is that I want a safety margin for degradation of
performance due to ohmic losses,
from errors in theory and from degraded element surfaces due to ageing.
With the weight factors that I have adopted as my favourites,
cz=0.005 and cl=10, the antenna labelled nice,
near optimum is obtained as the output of
the brute force optimisation.
For the "nice" antenna, the gain is 0.04dB below maximum on a
boom that is 4% longer.
These degradations allow a reduction of the losses by 35%
and a bandwidth increase of 39%.
If antennas are designed for some other band than 144MHz,
it is possible to change the equations to produce max G/T,
or whatever other combination of properties the
model is able to calculate for any given antenna geometry.
9. GAIN VS BOOM LENGTH FOR YAGI ANTENNAS.
With the "nice" parameters I have made a large number of
calculations on different numbers of elements and with
different stacking configurations.
In all these calculations I have chosen to make the element
diameters 10mm.
The 8 element design gives a gain figure of 12.47dBd on a 4.387m boom.
Fig 3 shows the gain of these antennas,
and a set of other ones [11] plotted against the boom length.
The "nice" antennas are about 0.5 dB better than typical
EME antennas of 3 to 5 wl boomlength.
For very long, or short booms the gain is about 1 dB above
the straight line of optimum antennas in [11].
For more than two years I have been using a
4-stack of 14 element cross yagis designed as described above.
I am very satisfied with the results,
good places in EME contests show that it is possible to get
these very high performance antennas to work in the real world.
Great care has to be taken however, and I will come back to that,
and to various numerical results, particularly related
to stacking, in a second article.
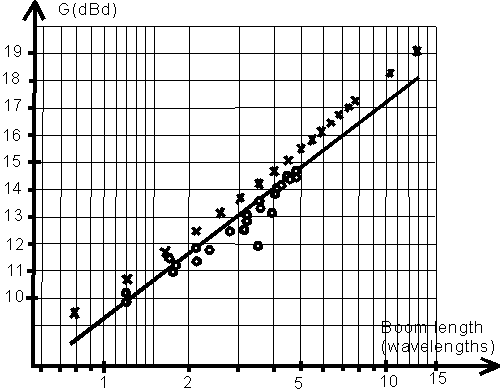
Fig 3. Yagi antenna gain at 144MHz versus boom length.
The dots and the straight line are from ref [11],
the crosses are the "nice" 50 ohm brute force designs.
References:
1. Roger F Harrington,"Matrix Methods for Field Problems,
" Proc. IEEE, Vol 55, No. 2, pp. 136-149; February 1967.
2. D. C. Kuo and B. J. Strait, "Improved programs for
analysis of radiation and scattering by configurations
of arbitrarily bent thin wires,". Syracuse University,
Syracuse, New York. Manuscript.
3. H. H. Chao and B. J. Strait, "Computer programs for
radiation and scattering by arbitrary configurations of
bent wires," Scientific Report No. 7 on Contract
F19628-68-C-0180, AFCRL-70-0374; Sept 1970.
4. D. C. Kuo and B. J. Strait, "A program for computing near
fields of thin wire antennas," Scientific report No. 14 on
Contract F19628-68-C-0180, AFCRL-71-0463; Sept 1971.
5. James L. Lawson, W2PV, "Yagi antenna design: performance
calculations," Ham Radio, Jan 1980, pp. 22-27.
6. C. A. Chen and D. K. Cheng,
"Optimum element lengths for Yagi-Uda arrays,"
IEEE Trans. Antennas Propagat.,
vol. AP-23, pp. 8 - 15, Jan 1975.
7. L. Asbrink,
"The optimum 6 element Yagi-antenna,"
VHF Communications, vol 14, No 1, Spring 1982.
8. N. Longsomboon, H. E. Green and J. D. Cashman, "Numerical
optimisation of Yagi-Uda arrays", Monitor - Proceedings of
the IREE Australia, Nov 1977.
9. P. E. Gill and W. Murray, "Algorithms for the solution
of the non - linear least - squares problem",
NPL Report NAC 71, 1976.
10. R. L. Fante, "Maximum possible gain for an arbitrary
ideal antenna with specified quality factor",
IEEE Trans. Antennas Propagat., vol. 40, pp. 1586 - 1588, Dec 1992.
11. Rainer Bertelsmeier, DJ9BV, "Gain and Performance
Data of 144 MHz Antennas", DUBUS-magazin, no 3, pp 181-189, 1988.
To SM 5 BSZ Main Page
| 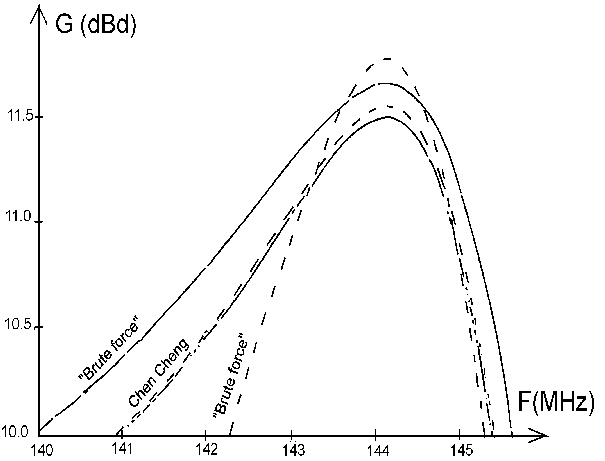 Fig 1. Gain above dipole vs frequency for the 6 element
Chen and Cheng design compared with the 6 element optimum antenna
produced by the brute force optimisation method.
1 dB gain bandwidth is indicated.
Solid lines are with ohmic losses included, and dotted lines are for
lossless antennas.
Fig 1. Gain above dipole vs frequency for the 6 element
Chen and Cheng design compared with the 6 element optimum antenna
produced by the brute force optimisation method.
1 dB gain bandwidth is indicated.
Solid lines are with ohmic losses included, and dotted lines are for
lossless antennas.
 Fig 2. Gain above dipole vs frequency for the 8 element design
by Longsomboon, Green and Cashman, compared with 8 element
optimum antennas produced by the brute force optimisation method.
The intermediate 7 element design is also shown, see text. -1 dB
gain bandwidth is indicated.
Fig 2. Gain above dipole vs frequency for the 8 element design
by Longsomboon, Green and Cashman, compared with 8 element
optimum antennas produced by the brute force optimisation method.
The intermediate 7 element design is also shown, see text. -1 dB
gain bandwidth is indicated.
